Skip to the Main Content

Note:These pages make extensive use of the latest XHTML and CSS Standards. They ought to look great in any standards-compliant modern browser. Unfortunately, they will probably look horrible in older browsers, like Netscape 4.x and IE 4.x. Moreover, many posts use MathML, which is, currently only supported in Mozilla. My best suggestion (and you will thank me when surfing an ever-increasing number of sites on the web which have been crafted to use the new standards) is to upgrade to the latest version of your browser. If that's not possible, consider moving to the Standards-compliant and open-source Mozilla browser.

October 23, 2011

A Math Puzzle Coming From Chemistry

Posted by John Baez

I posed this puzzle a while back over on Azimuth, and nobody solved it. Maybe it was too mathematical for most people there—it seems to be a problem in Klein geometry, actually. But also it’s a bit tricky: now that I think about it more, I’m not sure how to solve it either!

So, maybe you can help.

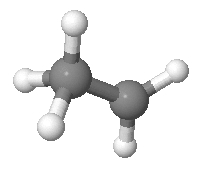
Suppose we have an ethyl cation. We’ll pretend it looks like this:

As I explained before, it actually doesn’t—not in real life. But never mind! Realism should never stand in the way of a good puzzle.

Continuing on in this unrealistic vein, we’ll pretend that the two black carbon atoms are distinguishable, and so are the five white hydrogen atoms. As you can see, 2 of the hydrogens are bonded to one carbon, and 3 to the other. We don’t care how the hydrogens are arranged, apart from which carbon each hydrogen is attached to. Given this, there are

2×(52)=20 2 \times \displaystyle{ \binom{5}{2} = 20 }

ways to arrange the hydrogens. Let’s call these arrangements states.

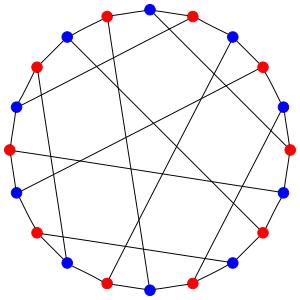
Now draw a dot for each of these 20 states. Draw an edge connecting two dots whenever you can get from one state to another by having a hydrogen hop from the carbon with 2 hydrogens to the carbon with 3. You’ll get this picture, called the Desargues graph:

The red dots are states where the first carbon has 2 hydrogens attached to it; the blue ones are states where the second carbon has 2 hydrogens attached to it. So, each edge goes between a red and a blue dot. And there are 3 edges coming out of each dot, since there are 3 hydrogens that can make the jump!

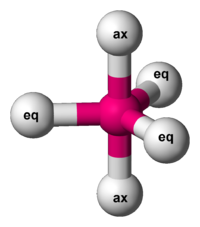
Now, the puzzle is to show that you can also get the Desargues graph from a different kind of molecule. Any molecule shaped like this will do:

The 2 balls on top and bottom are called axial, while the 3 around the middle are called equatorial.

There are various molecules like this. For example, phosphorus pentachloride. Let’s use that.

Like the ethyl cation, phosphorus pentachloride also has 20 states… but only if count them a certain way! We have to treat all 5 chlorines as distinguishable, but think of two arrangements of them as the same if we can rotate one to get the other. Again, I’m not claiming this is physically realistic: it’s just for the sake of the puzzle.

Phosphorus pentachloride has 6 rotational symmetries, since you can turn it around its axis 3 ways, but also flip it over. So, it has

5!6=20 \displaystyle{ \frac{5!}{6} = 20}

states.

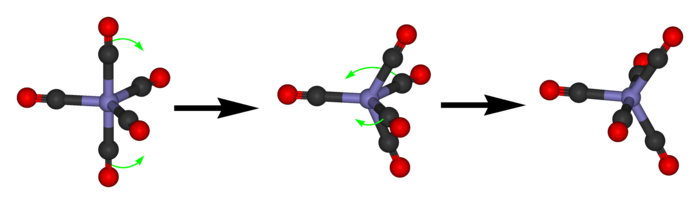
That’s good: exactly the number of dots in the Desargues graph! But how about the edges? We get these from certain transitions between states. These transitions are called pseudorotations, and they look like this:

Phosphorus pentachloride really does this! First the 2 axial guys move towards each other to become equatorial. Beware: now the equatorial ones are no longer in the horizontal plane: they’re in the plane facing us. Then 2 of the 3 equatorial guys swing out to become axial.

To get from one state to another this way, we have to pick 2 of the 3 equatorial guys to swing out and become axial. There are 3 choices here. So, we again get a graph with 20 vertices and 3 edges coming out of each vertex.

Puzzle. Is this graph the Desargues graph? If so, show it is.

I read in some chemistry papers that it is. But is it really? And if so, why? David Corfield suggested a promising strategy. He pointed out that we just need to get a 1-1 correspondence between

• states of the ethyl cation and states of phosphorus pentachloride,

together with a compatible 1-1 correspondence between:

• transitions of the ethyl cation and transitions of phosphorus pentachloride.

And he suggested that to do this, we should think of the split of hydrogens into a bunch of 2 and a bunch of 3 as analogous to the split of chlorines into a bunch of 2 (the ‘axial’ ones) and a bunch of 3 (the ‘equatorial’ ones).

It’s a promising idea. There’s a problem, though! In the ethyl cation, a single hydrogen hops from the bunch of 3 to the bunch of 2. But in a pseudorotation, two chlorines go from the bunch of 2 to the bunch of 3… and meanwhile, two go back from the bunch of 3 to bunch of 2.

And if you think about it, there’s another problem too. In the ethyl cation, there are 2 distinguishable carbons. One of them has 3 hydrogens attached, and one doesn’t. But in phosphorus pentachloride it’s not like that. The 3 equatorial chlorines are just that: equatorial. They don’t have 2 choices about how to be that way. Or do they?

Well, there’s more to say, but this should already make it clear that getting ‘natural’ one-to-one correspondences is a bit tricky… if it’s even possible at all!

We could try solving the problem using the ideas behind Felix Klein’s ‘Erlangen program’. The group of permutations of 5 things, say S 5,S_5, acts as symmetries of either molecule. For the ethyl cation the set of states will be X=S 5/GX = S_5/G for some subgroup G.G. You can think of XX as a set of structures of some sort on a 5-element set. The group S 5S_5 acts on XX, and the transitions will give an invariant binary relation on XX. For phosphorus pentachloride we’ll have some set of states X′=S 5/G′X\prime = S_5/G\prime for some other subgroup G′G\prime, and the transitions will give an invariant relation on X′X\prime.

We could start by trying to see if GG is the same as G′G\prime—or more precisely, conjugate. If they are, that’s a good sign. And if not, it’s bad: it probably means there’s no ‘natural’ way to show the graph for phosphorus pentachloride is the Desargues graph… so maybe it’s not true.

I could say more, but I’ll stop here.

Posted at October 23, 2011 11:37 AM UTC

TrackBack URL for this Entry:   https://golem.ph.utexas.edu/cgi-bin/MT-3.0/dxy-tb.fcgi/2449



14 Comments & 0 Trackbacks

Re: A Math Puzzle Coming From Chemistry

I could say more

You could and did – there was an extra sentence or two that you edited out from the Azimuth version!

You probably had your reasons… :-)

Posted by: Todd Trimble on October 23, 2011 1:16 PM | Permalink | Reply to this

Re: A Math Puzzle Coming From Chemistry

I don’t know what those sentences are… I edited both versions about 8 times, tweaking lots of sentences, deciding whether or not to burden the Azimuth readers with terms like “invariant relation”, whether or not to insult the nn-Café readers with remarks like “If you know some group theory”, etc.

Posted by: John Baez on October 23, 2011 1:41 PM | Permalink | Reply to this

Re: A Math Puzzle Coming From Chemistry

The words I was referring to are these: “In case you’re wondering, all this is just a trick to get more mathematicians interested in chemistry. A few may then go on to do useful things.”

Posted by: Todd Trimble on October 23, 2011 3:01 PM | Permalink | Reply to this

Re: A Math Puzzle Coming From Chemistry

Busted, John!

:-)

Posted by: Tom Leinster on October 23, 2011 4:45 PM | Permalink | Reply to this

Re: A Math Puzzle Coming From Chemistry

Oh, that. Yeah, over on Azimuth I usually try to avoid pure math and feel the need to apologize for it, but over here it’s sort of the point, so I should apologize for apologizing for it. A mathematician’s apology is never done.

Posted by: John Baez on October 24, 2011 3:53 AM | Permalink | Reply to this

Re: A Math Puzzle Coming From Chemistry

In the ethyl cation, a single hydrogen hops from the bunch of 3 to the bunch of 2.

That is not true. Suppose that hydrogens a,b are on the first carbon, while c,d,e are on the second. When c moves to the first, a,b,c becomes the bunch of 3, while d,e become the bunch of 2. So a,b moved from 2 to 3, while d,e moved from 3 to 2. The hydrogen c that physically moves is the only one that stays in the same state!

Posted by: Twan van Laarhoven on October 23, 2011 1:17 PM | Permalink | Reply to this

Re: A Math Puzzle Coming From Chemistry

John wrote:

In the ethyl cation, a single hydrogen hops from the bunch of 3 to the bunch of 2.

Twan wrote:

That is not true.

It is if you interpret my words the way I meant them to be interpreted.

I meant that a single hydrogen hops from what is initially the bunch of 3 to what is initially the bunch of 2. But course after it’s made that hop, what was initially the bunch of 2 has become a bunch of 3… and what was initially the bunch of 3 has become a bunch of 2!

However, your interpretation of my words is the basis of this trick.

Posted by: John Baez on October 23, 2011 1:38 PM | Permalink | Reply to this

Re: A Math Puzzle Coming From Chemistry

We’re seeing some nice progress over here.

Posted by: John Baez on October 23, 2011 1:30 PM | Permalink | Reply to this

Re: A Math Puzzle Coming From Chemistry

I haven’t followed the other thread - I gather that you have now solved the problem over there - but I thought it would be fun to try to work out the bijection on my own. Undoubtedly the following reproduces your results.

In the phosphorus pentachloride problem we can represent a configuration as an ordered list (a,b,c,d,e) where a, b, c are the equatorial atoms listed in some order, d is the axial atom in the direction given by the right-hand-rule applied to configuration (a,b,c), and e is the other axial atom. Because of equivalence of configurations under rotation, we should consider (a,b,c,d,e) and (v,w,x,y,z) to be equivalent if the following conditions hold:
(1) (v,w,x) is a permutation of (a,b,c),
(2) (y,z) is a permutation of (d,e)
(3) (a,b,c,d,e) and (v,w,x,y,z) are even permutations of each other.
The implication of (3) is that the even permutations of (a,b,c), which are cyclic, leave d and e fixed, whereas the odd permutations of (a,b,c), which correspond to flips, interchange d and e. This is exactly how rotations should act.

The pseudorotation corresponds to the map (a,b,c,d,e) |→ (a,d,e,c,b), which is an odd permutation of (a,b,c,d,e). (There are, of course, two other pseudorotations, which are obtained by cyclically permuting (a,b,c).)

In the ethyl cation problem, we can represent configurations using the same ordered lists, and the same notion of equivalence, as in the phosphorus pentachloride problem. This works as follows: a, b, c are the atoms in the group of three, and d, e are the atoms in the group of two. We adopt the convention that the group of three sits on carbon 1 if the permutation is even, and on carbon 2 if the permutation is odd. The notion of equivalence is the correct one since it preserves the grouping of the atoms as well as the carbon atom on which they are situated.

A hop of atom a to the other carbon atom is descibed, once again, by the map (a,b,c,d,e)|→(a,d,e,c,b). One can see that, after this move, atom a sits with d and e, and, because the sign of the permutation has changed, it has moved to the other carbon atom. (Again, there are two other hops, those of atoms b and c, which are obtained by cyclically permuting (a,b,c).)

Posted by: Will Orrick on October 24, 2011 1:14 AM | Permalink | Reply to this

Re: A Math Puzzle Coming From Chemistry

Will Orrick wrote:

Because of equivalence of configurations under rotation, we should consider (a,b,c,d,e) and (v,w,x,y,z) to be equivalent if the following conditions hold:

(1) (v,w,x) is a permutation of (a,b,c),

(2) (y,z) is a permutation of (d,e)

(3) (a,b,c,d,e) and (v,w,x,y,z) are even permutations of each other.

The implication of (3) is that the even permutations of (a,b,c), which are cyclic, leave d and e fixed, whereas the odd permutations of (a,b,c), which correspond to flips, interchange d and e. This is exactly how rotations should act.

Great! This is precisely the subtlety that makes the problem sort of tricky.

I like to think about this sort of problem in terms of ‘finite sets with extra structure’. A state of phosphorus pentachloride consists of taking the set {1,2,3,4,5}\{1,2,3,4,5\} and equipping it, first with a partition into a 2-element set and a 3-element set, and then one extra bit of information. But what is this extra bit of information?

It’s not a 2-coloring of the 2-element set, and it’s not a cyclic ordering on the 3-element set. It’s an interesting ‘blend’ of the two!

Namely, for each 2-coloring of the 2-element set you pick a cyclic ordering of the 3-element set, such that if you change the 2-coloring you also have to change the cyclic ordering!

Over on Azimuth I explained this as follows:

You just mentioned two very tempting ways to introduce an extra bit of information into the phosphorus pentachloride problem. But we don’t get to pick how to introduce that extra bit of information: the puzzle as stated tells us how we have to do it!

The puzzle says that two molecules of phosphorus pentachloride with chlorine atoms labelled 1,2,3,4,5 count as being in the same state if we can rotate one to the other, carrying the labelling of one to the labelling of the other.

So, the two axial positions are not distinguishable: we can always rotate the molecule so that the ‘top’ chlorine becomes the ‘bottom’ one, and vice versa.

Similarly, the two cyclic orderings of the three equatorial chlorines are not distinguishable: we can always rotate the molecule so that the ‘clockwise’ cyclic ordering becomes the ‘counterclockwise’ one, and vice versa.

However, you’ll note that flipping the molecule over to make the top chlorine the bottom one also changes the clockwise cyclic ordering into the counterclockwise one.

So while neither of your ways of introducing an extra bit of information is the way prescribed by the problem, the sum of these two bits is. (Here I’m adding bits mod 2.)

So the mini-puzzle is whether this bit inevitably changes when we do a pseudorotation.

And the answer is yes.

Posted by: John Baez on October 24, 2011 4:30 AM | Permalink | Reply to this

Re: A Math Puzzle Coming From Chemistry

As some comments have pointed out over on Azimuth, in both cases there are ten underlying states which simply pick out two of the five pendant atoms as special, together with an extra parity bit (which can take either value for any of the ten states), giving twenty states in total. The correspondence of the ten states is clear: an edge exists between state A and state B, in either case, if and only if the two special atoms of state A are disjoint from the two special atoms of state B. This is precisely one definition of the Petersen graph (a famous 3-valent graph on 10 vertices that shows up as a small counterexample to lots of na¯ve conjectures). Thus the graph in either case is a double cover of the Petersen graph–but that does not uniquely specify it, since, for example, both the Desargues graph and the dodecahedron graph are double covers of the Petersen graph.

For a labeled graph, each double cover corresponds uniquely to an element of the Z/2Z cohomology of the graph (for an unlabeled graph, some of the double covers defined in this way may turn out to be isomorphic). Cohomology over Z/2Z takes any cycle as input and returns either 0 or 1, in a consistent way (the output of a Z/2Z sum of cycles is the sum of the outputs on each cycle). The double cover has two copies of everything in the base (Petersen) graph, and as you follow all the way around a cycle in the base, the element of cohomology tells you whether you come back to the same copy (for 0) or the other copy (for 1) in the double cover, compared to where you started.

One well-defined double cover for any graph is the one which simply switches copies for every single edge (this corresponding to the element of cohomology which is 1 on all odd cycles and 0 on all even cycles). This always gives a double cover which is a bipartite graph, and which is connected if and only if the base graph is connected and not bipartite. So if we can show that in both cases (the fictitious ethyl cation and phosphorus pentachloride) the extra parity bit can be defined in such a way that it switches on every transition, that will show that we get the Desargues graph in both cases.

The fictitious ethyl cation is easy: the parity bit records which carbon is which, so we can define it as saying which carbon has three neighbors. This switches on every transition, so we are done. Phosphorus pentachloride is a bit trickier; the parity bit distinguishes a labeled molecule from its mirror image, or enantiomer. As has already been pointed out on both sites, we can use the parity of a permutation to distinguish this, since it happens that the orientation-preserving rotations of the molecule, generated by a three-fold rotation acting as a three-cycle and by a two-fold rotation acting as a pair of two-cycles, are all even permutations, while the mirror image that switches only the two special atoms is an odd permutation. The pseudorotation can be followed by a quarter turn to return the five chlorine atoms to the five places previously occupied by chlorine atoms, which makes it act as a four-cycle, an odd permutation. Since the parity bit in this case also can be defined in such a way that it switches on every transition, the particular double cover in each case is the Desargues graph–a graph I was surprised to come across here, since just this past week I have been working out some combinatorial matrix theory for the same graph!

The five chlorine atoms in phosphorus pentachloride lie in six triangles which give a triangulation of the 2-sphere, and another way of thinking of the pseudorotation is that it corresponds to a Pachner move or bistellar flip on this triangulation–in particular, any bistellar flip on this triangulation that preserves the number of triangles and the property that all vertices in the triangulation have degree at least three corresponds to a pseudorotation as described.

Posted by: Tracy Hall on October 24, 2011 3:00 AM | Permalink | Reply to this

Re: A Math Puzzle Coming From Chemistry

Wow, that’s a great solution, Tracy! I would never thought of the connection to Pachner moves, though I know and love Pachner moves. And it’s cool how you classified the double covers of the marvelous Petersen graph:
I took the liberty of copying your answer over to Azimuth, so people scared of coming here could see it.
Posted by: John Baez on October 24, 2011 4:10 AM | Permalink | Reply to this

Re: A Math Puzzle Coming From Chemistry

I’ve written up a simple and I hope correct solution to the puzzle here.

Posted by: John Baez on October 25, 2011 8:56 AM | Permalink | Reply to this

Re: A Math Puzzle Coming From Chemistry

In both cases S_5 acts transitively on a set with 20 elements, and you can find an element such that the stabilizer is S_2 x S_3.

Posted by: David Lehavi on October 26, 2011 1:44 PM | Permalink | Reply to this

Post a New Comment