Modeling Surface Diagrams
Posted by Simon Willerton
Note This is reposted from the temporary site so that comments can continue here.
I’m currently at MSRI at a knot homology meeting. There are lots of people here with pictures of surfaces, some of these even being categorical, so I thought I would return to the subject of computer manipulation of these. In particular I thought I would make use of our (hopefully) brief sojourn at WordPress and take the opportunity to embed some videos (but then I was told how I could do it at our usual place).
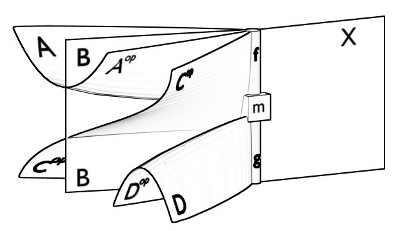
In my paper A diagrammatic approach to Hopf monads I had lots and lots of surface diagrams – these are the one-dimension higher version of string diagrams which can be useful for notating morphisms in monoidal 2-categories or 3-categories. So I had to draw two hundred or so pictures like this one.

[I hope to write something more about Hopf monads at the café at some point very soon.]
I drew all of these pictures in xfig – a standard 2-dimensional drawing package in which you have to do all of the 3-d stuff by eye and can’t do any fancy shading or anything. It would be really nice if I could actually create these as 3-d objects and then just export some projection of them, possibly suitably ray traced. I had an attempt at creating some categorical surfaces using blender, which is a splendid piece of open source software which you can use to make movies like Shrek or Monsters Inc. Here are two of my efforts.
The first represents the associator natural transformation in a monoidal category (see the Hopf monads paper linked above for the details).
The second is the so-called swallowtail relation (see Figure 25 on page 40 of HDA4).
As well making movies with such models you can also embed the 3d model in to pdf files and, provided you’re using acrobat(!), your readers can rotate the surface for themselves. Here’s an example from meshlab.
Whilst this is all well and good, there are at least two things I would like to be able to do that I currently can’t.
- Draw on the surfaces. I want to be able to draw what are essentially morphisms, like in the Hopf monad picture above, and also to be able to label them.
- Integrate with mathematics software such as sage or maple, or possibly even with some scripting language such a python. Then I wouldn’t have to input the surfaces with a mouse incredibly slowly in blender, but would be able to somehow code up the surfaces.
One thing to note is that these “surfaces” can be singular, as in the associator example above, so are not so easy to handle in standard packages with tend to expect non-singular things.
So, has anyone else tried using 3d software for modeling surface diagrams?


Re: Modeling Surface Diagrams
You have always been able to embed YouTube videos. You just have to do it right.