Skip to the Main Content

Note:These pages make extensive use of the latest XHTML and CSS Standards. They ought to look great in any standards-compliant modern browser. Unfortunately, they will probably look horrible in older browsers, like Netscape 4.x and IE 4.x. Moreover, many posts use MathML, which is, currently only supported in Mozilla. My best suggestion (and you will thank me when surfing an ever-increasing number of sites on the web which have been crafted to use the new standards) is to upgrade to the latest version of your browser. If that's not possible, consider moving to the Standards-compliant and open-source Mozilla browser.

November 17, 2010

Alice!

Tonight, the ALICE collaboration released their first paper. This must be something of a record, as they just started observing Pb-Pb collisions on Nov. 7.

They’ve observed elliptic flow at center-of-mass-energy/nucleon-pair s NN=2.76\sqrt{s_{NN}}= 2.76 TeV. For those who were sceptical, the quark-gluon plasma is still a strongly-coupled liquid, with very low shear viscosity, at LHC energies — more than a order of magnitude larger than the s NN=200\sqrt{s_{NN}}= 200 GeV at RHIC.

As with the proton-proton experiments, they are currently operating at only half the design energy. But, unlike proton-proton, which beat the Tevatron by only a modest factor, the heavy-ion experiments are already probing energies an order-of-magnitude larger than those seen at RHIC.

Below is one of their plots (for v 2v_2, integrated over p tp_t). v 2v_2 is the coefficient of cos(2ϕ)\cos(2\phi) in a Fourier series of the azimuthal dependence of the particle multiplicity produced in the collision; the larger v 2v_2, the stronger the elliptic flow.

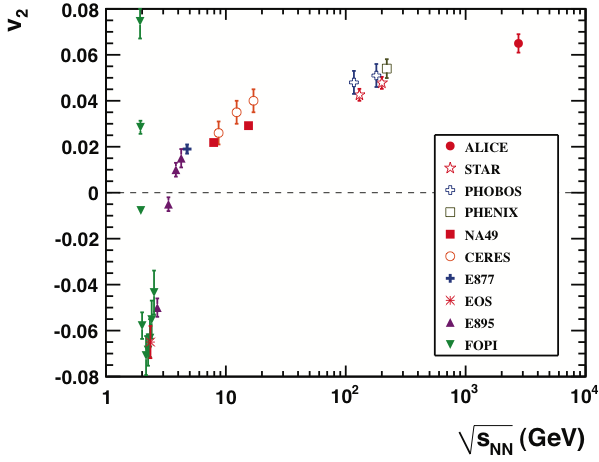
v_2, integrated over p_t, at ALICE and previous experiments
Integrated elliptic flow at 2.76 TeV in Pb-Pb 20-30% centrality class compared with results from lower energies taken at similar centralities
Posted by distler at November 17, 2010 11:31 PM

TrackBack URL for this Entry:   https://golem.ph.utexas.edu/cgi-bin/MT-3.0/dxy-tb.fcgi/2303



12 Comments & 1 Trackback

Read the post ALICE Publishes!
Weblog: Asymptotia
Excerpt: Jacques Distler pointed out that ALICE has just published their first paper, only a little over a week after the beginning of the heavy ion phase of the LHC at CERN! Moreover, they are way ahead in energy of the previous heavy ion collision experiment ...
Tracked: November 18, 2010 12:45 AM

Re: Alice!

A question off topic: what do you think about renormalizations, Jacques? Is it a legitimate and unique means for doing calculations?

Do you believe that we will be able to construct theories without necessity to renormalize them?

Thanks,

Vladimir.

Posted by: Vladimir Kalitvianski on November 19, 2010 5:54 AM | Permalink | Reply to this

Re: Alice!

If you don’t appreciate Wilson’s insight into the meaning of renormalization (and the Renormalization Group), then you don’t understand quantum field theory.

So I think your question is ill-posed.

To be fair, the Wilsonian approach is still not sufficiently emphasized in the textbooks. So, it remains possible (maybe even likely) for someone to get through a year-long course in QFT, without any exposure to this topic.

Anyone who has some reading suggestions for Vladimir can feel free to chime in.

Posted by: Jacques Distler on November 19, 2010 8:09 AM | Permalink | PGP Sig | Reply to this

Re: Alice!

Thanks, Jacques, for your answer. I know about K. Wilson’s insight. It is not convincing to me, to tell the truth.

I consider those infinities to be a second sign of badly guessed theory. The first sign is easily seen in the first Born approximation, even before encountering divergences. Let us look at any elastic cross section in QED (Mott, Bhabha, Rosenbluth, and Klein-Nishina): first they are finite, then they are IR divergent; in higher orders they are divergent even more and more, whereas the exact values are just equal to zero. These first-Born-approximation results are presented as a success despite crying absence of soft radiation in them. The most probable phenomenon - soft radiation, is missing in them. An the least probable event (elastic scattering) is different from zero. Then calculations encounter difficulties - divergent contributions. It is so because no warning is noticed in the first Born approximation. Thus, I think, the theory has a very bad start - its initial approximation is “too distant” from the exact solution, it does not catch correctly the most probable physical phenomena because the charge is decoupled from the field subsystem. This is the true reason of divergences in QED, in my opinion.

Regards,

Vladimir.

http://groups.google.com/group/qed-reformulation

http://vladimirkalitvianski.wordpress.com/

Posted by: Vladimir Kalitvianski on November 19, 2010 11:05 AM | Permalink | Reply to this

Wilson

Infrared divergences are a sign that you asked an unphysical question.

UV divergences are a sign that — even if your question was sensible — your computation of the answer made unwarranted assumptions about short-distance physics, of which you are in fact ignorant.

Wilson gives you a way to organize your ignorance of short-distance physics in a useful way.

If you think you are God, then I suppose you might feel justified in dispensing with Wilson. For the rest of us, Wilson is indispensable to understanding what quantum field theory means. Short of a God-like knowledge of short-distance physics, renormalization is an inevitable part of what it means to do quantum field theory.

Sorry, but that is just the way the world works, and (unless you want to waste your time barking up the wrong tree) you’d better get used to it.

Posted by: Jacques Distler on November 19, 2010 11:28 AM | Permalink | PGP Sig | Reply to this

Re: Alice!

Thank you, Jacques, you’ve answered my questions.

Concerning me, I do not ask unphysical questions. The elastic cross section is a quite physical notion and it is always different from zero if there is a threshold in exciting the “internal” degrees of freedom of a target. In QED the answer is known too - it is zero in the end.

Regards,

Vladimir.

Posted by: Vladimir Kalitvianski on November 19, 2010 11:42 AM | Permalink | Reply to this

Re: Alice!

By the way, in order to dispense with K. Wilson approach, it is not necessary to be a god. I think there are no many secrets of physics at short distances in QED. At least, I see it quite differently than K. Wilson.

Regards,

Vladimir.

Posted by: Vladimir Kalitvianski on November 19, 2010 2:15 PM | Permalink | Reply to this

Wilson

I think there are no many secrets of physics at short distances in QED.

That’s because you are already pretending to be God (or deceiving yourself).

A nice example to work through is QED with two charged fermions, one heavy (“the muon”) and one light (“the electron”).

At low energies (ie, much below the muon mass) you — as a low-energy physicist — don’t know whether the muon exists, much less what its mass is. But everything that you don’t know about high energy physics should be summarized in the low-energy effective Lagrangian involving the electron and the electromagnetic field alone.

Wilson (or Weinberg or whoever) tells you how to do that. It’s worth learning how to reconcile the computation (say) of the anomalous magnetic moment of the electron in the effective theory (without the muon) with the calculation done in the “full” theory (with the muon).

This is just a toy model, of the real world, where we really don’t know what degrees of freedom are present at high energies. But Wilson tells you that, despite that ignorance, it’s possible to do reliable calculations at low energies – provided you organize them correctly.

Sorry, but if you think you can dispense with renormalization in QFT, then you are either making unwarranted assumptions about short-distance physics, or you are fooling yourself (most likely, both).

Posted by: Jacques Distler on November 19, 2010 4:37 PM | Permalink | PGP Sig | Reply to this

Wilson

No, Jacques, everything is much simpler. And please, do not call me a god as well as a barking dog. Stay polite.

As to a toy model, I have a nice one that works fine without mathematical and conceptual difficulties, unlike QED. At the same time, one can see that high-energy extra excitations can be easily added without problems, if necessary.

It is another formulation, and I think, it is much more physical. It proceeds from a permanently coupled charge and its EMF and it does not have a self-action. Agree, if one uses another initial approximation, the corresponding perturbative series are different, even in the frame of the same problem. There is nothing bad, god- or dog-like if I have such an experience.

Concerning Wilson’s insight, K. Wilson starts from an effective theory by definition so he is bound to arrive at the same conclusion - his theory is effective, not exact. It does not shed the light on the true QFT problems.

> that is just the way the world works, and you’d better get used to it.

Our trial models are not “the world”, do not exaggerate.

Regards,

Vladimir.

Posted by: Vladimir Kalitvianski on November 20, 2010 5:46 AM | Permalink | Reply to this

Re: Alice!

When I created everything, self-symmetry seemed the easiest way to make it all work, so now we’re all stuck with renormalization. I probably could have done better, but I had animals to create, the Tree of the Fruit of Knowledge was way behind schedule and over budget, and the Shabbos was coming up. I’m sorry if this is causing you headaches now, Vladimir. Next time I slam a few branes together, I’ll try to do better.

God

PS Just kidding about the branes. They’re not real. :)

Posted by: God on December 18, 2010 12:52 AM | Permalink | Reply to this

Reformulation instead of Renormalization

Too bad that you cannot seriously discuss this issue.

If a numerical solution diverges in course of iterations, it is not the computer who is guilty but the physicist who programmed such a numerical scheme. It can easily happen if one starts from a very bad initial approximation. Similarly in case of analytical iterations: divergences generally appear as a sign of a wrong physical and/or mathematical approach to the problem being solved.

Posted by: Vladimir Kalitvianski on December 19, 2010 11:02 AM | Permalink | Reply to this

Re: Reformulation instead of Renormalization

“God”: Please don’t feed the trolls.

Valdimir: We have heard quite enough about your “theories.” I will delete further comments on that topic.

Pure QED is trivial as a continuum QFT. The proof is elementary, and can be found on pages 1-2 of hep-th/9511154. This, of course, does not stop us from using it as an effective QFT, whose UV completion involves additional degrees of freedom.

Posted by: Jacques Distler on December 19, 2010 11:37 AM | Permalink | PGP Sig | Reply to this

Re: Reformulation instead of Renormalization

Renormalized and IR-fixed pure QED does not need a UV completion. It works fine at L–>infinity without limitation.

QED may be made a part of another theory but currently it is a self-sufficient theory. Another matter, it is not self-consistent but nevertheless its final results are fine.

What I write is not trolling; it is just off topic with respect to the “ALICE!” subject.

Thank you for your answers, Jacques. So long.

Vladimir.

Posted by: Vladimir Kalitvianski on December 19, 2010 3:18 PM | Permalink | Reply to this

Post a New Comment