Skip to the Main Content

Note:These pages make extensive use of the latest XHTML and CSS Standards. They ought to look great in any standards-compliant modern browser. Unfortunately, they will probably look horrible in older browsers, like Netscape 4.x and IE 4.x. Moreover, many posts use MathML, which is, currently only supported in Mozilla. My best suggestion (and you will thank me when surfing an ever-increasing number of sites on the web which have been crafted to use the new standards) is to upgrade to the latest version of your browser. If that's not possible, consider moving to the Standards-compliant and open-source Mozilla browser.

July 31, 2008

Best Fit

Via Tommaso Dorigo, Pete Renton’s talk at ICHEP08, a report on Global Electroweak Fits and the Higgs Boson Mass. Incorporating the latest Tevatron data,

  • m t=172.5±1.2m_t = 172.5\pm 1.2 GeV.
  • m W=80.413±0.048m_W = 80.413\pm 0.048 GeV.
  • α s(M Z 2)=0.1185±0.0026\alpha_s(M_Z^2) = 0.1185 \pm 0.0026
  • m H<154m_H \lt 154 GeV at the 95%95\% confidence level.
  • m H=84 −26 +34m_H = 84^{+34}_{-26} GeV (highly sensitive to m Wm_W and M tM_t).
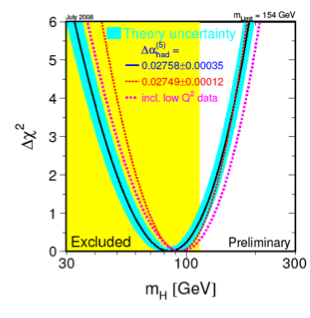
Higss mass χ-squared fit

The data seem to heavily favour a light Higgs.

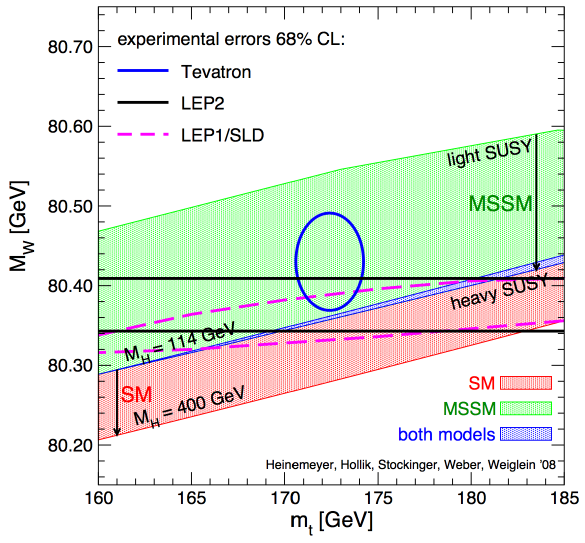
The most striking plot, however, from Dorigo’s post, was not in Renton’s talk. It comes from Heinemeyer et al, and the theoretical analysis behind it is explained here.

The red band, corresponding to the Standard Model, comes from varying the only free parameter in the model, m Hm_H, from the LEP exclusion bound, m H>114m_H\gt 114 GeV, up to m H=400m_H=400 GeV. The green band corresponds to the unconstrained MSSM. The upper edge corresponds to the region where m t˜ 2/m t˜ 1m_{\tilde{t}_2}/m_{\tilde{t}_1} and/or m b˜ 2/m b˜ 1>2.5m_{\tilde{b}_2}/m_{\tilde{b}_1}\gt 2.5. The lower edge corresponds to the decoupling limit, where all the superpartners are heavy.

The Tevatron seems to mildly favour the MSSM over the SM.

W mass versus top mass

While precision electroweak fits are nice, direct search results are nicer. Via Matt Reece, comes news that D0 has excluded (ppt), at 2σ\sigma, m Hm_H in a narrow range centered at 170 GeV. There’s also a summary of the combined CDF/D0 limits on m H>155m_H\gt 155 GeV.

1 We work in the convention that m f˜ 2/m f˜ 1≥1m_{\tilde{f}_2}/m_{\tilde{f}_1}\geq 1

Posted by distler at July 31, 2008 4:34 PM

TrackBack URL for this Entry:   https://golem.ph.utexas.edu/cgi-bin/MT-3.0/dxy-tb.fcgi/1757



1 Comment & 0 Trackbacks

yukawa coupling

The new value of top mass implies thus a yukawa coupling of

y_t= 0.9902 \pm 0.0073

I keep amazed about how the old susy running prediction “y_t has order unity” got a precision two orders of magnitude beyond expectations.

Posted by: Alejandro Rivero on July 31, 2008 5:10 PM | Permalink | Reply to this

Post a New Comment