WMAP Results
WMAP has released their 2nd and 3rd year data.
The measurements of the CMBR anisotropy show clear signs of the 3rd acoustic peak.
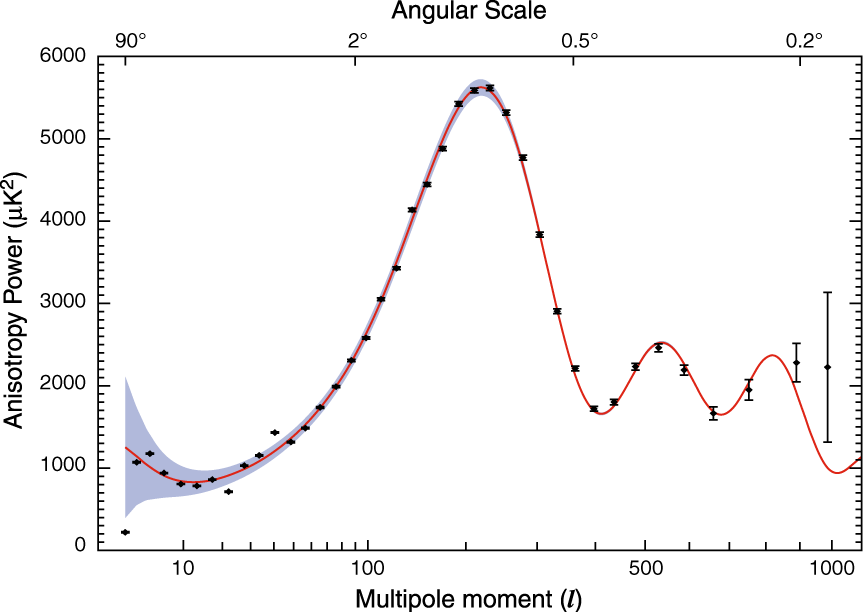 WMAP CMBR power spectrum, for multipole moments, .
WMAP CMBR power spectrum, for multipole moments, .On the subject of polarization, they find no evidence for -modes and an upper limit on the scalar/tensor ratio, , which is getting close to the predictions of simple inflationary models, .
The fit to the ΛCDM model has improved markedly over the first year results.
Best fit for Cosmological Parameters from WMAP Year 3
| Parameter | WMAP Only | WMAP +CBI+VSA | WMAP
+ACBAR +BOOMERanG | WMAP +2dFGRS |
|---|
|
|
|
|
|
|---|
|
|
|
|
|
|---|
|
|
|
|
|
|---|
|
|
|
|
|
|---|
|
|
|
|
|
|---|
|
|
|
|
|
|---|
|
|
|
|
|
|---|
|
|
|
|
|
|---|
- (fractional) energy density in baryons
- (fractional) energy density in matter
- spectral density of scalar fluctuations
- amplitude of density fluctuations (/Mpc)
- reionization optical depth
- linear theory amplitude of matter fluctuations at Mpc
The full list of papers, doubtless contains more nuggets of information. Perhaps our cosmologist friends over at CosmicVariance will provide some insight.
Posted by distler at March 16, 2006 1:44 PM
TrackBack URL for this Entry: https://golem.ph.utexas.edu/cgi-bin/MT-3.0/dxy-tb.fcgi/769
 WMAP CMBR power spectrum, for multipole moments, .
WMAP CMBR power spectrum, for multipole moments, .

Re: WMAP Results
Jacques,
Just a heads-up: The WMAP Power Spectrum picture (the first one on your post) does not seem to be showing… and, in fact, if you try to actually open the image file, it complains that the file does not exist.
[]’s.