3d Rotations and the 7d Cross Product (Part 2)
Posted by John Baez
On Mathstodon, Paul Schwahn raised a fascinating question connected to the octonions. Can we explicitly describe an irreducible representation of on 7d space that preserves the 7d cross product?
I explained this question here:
This led to an intense conversation involving Layra Idarani, Greg Egan, and Paul Schwahn himself. The result was a shocking new formula for the 7d cross product in terms of the 3d cross product.
Let me summarize.
There are two equivalent ways to say what’s been done:
Theorem 1. We can explicitly describe an subgroup of such that the 7d irreducible representation of remains irreducible when restricted to this subgroup.
Theorem 2. We can explicitly describe an irreducible representation of on the imaginary octonions that preserves their dot product and cross product.
These are equivalent thanks to several well-known facts. The group of automorphisms of the octonions is . Its action on the space of imaginary octonions, , is the unique 7d irreducible representation of . This action preserves the usual dot product and cross product of imaginary octonions, given by
Conversely, any linear transformation of that preserves the cross product also preserves the dot product, and all such transformations come from the action of .
Either way we state the theorem, the only novelty — if any — is that we now have an explicit description. The existence seems to go back to old work by Dynkin:
- E. B. Dynkin, Semisimple subalgebras of semisimple Lie algebras, American Mathematical Society Translations, Series 2, Volume 6, 1957.
In fact we seem to have two explicit descriptions. Unfortunately it takes some serious calculation to prove that either of them actually works. I think a truly conceptual proof still awaits us, though the second description points a way forward.
Our first description will start by building the unique 7-dimensional irreducible representation of in a familiar way. Then we will equip it with an isomorphism to , and proof that the resulting action of on preserves the dot product and cross product. Layra Idarani proved this using fairly brutal calculations, which Greg Egan checked using Mathematica.
We start with the 3-dimensional inner product space with orthonormal basis . Then we let be the space of harmonic homogeneous degree-3 polynomials in and . This is 7-dimensional, since it has a basis
Since has an inner product we get an isomorphism , so we can also think of these polynomials as functions on . acts on functions on , preserving the conditions of being harmonic and homogeneous of degree 3, so it acts on . This is well-known to give the unique 7-dimensional irreducible representation of .
The next step is to choose a vector space isomorphism between and . For this, we use a well-known orthonormal basis of the imaginary octonions:
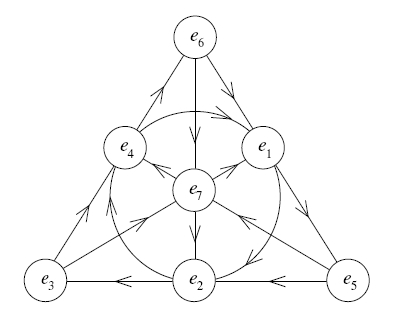
This pictures shows the Fano plane, with 7 points and 7 lines (one of which is drawn as a circle). Each line contains 3 points, and the arrows indicate a cyclic ordering of these 3 points. Each point corresponds to a basis element of the imaginary octonions. The cross product obeys
whenever are a cyclically ordered triple of points on a line. For example, and , but because the cross product is anticommutative.
Layra Idarani chose this isomorphism between and :
Using rather lengthy calculations, Layra and Greg checked that if we use this isomorphism to transfer the cross product on to , we get a cross product on that is -invariant.
Besides the calculations required, the main downside to this argument is that it relies on cleverly choosing an isomorphism . Luckily, Paul Schwahn came up with a second approach that elegantly defines a cross product on without choosing an isomorphism . Alas, it still requires a hard calculation to show this cross product is isomorphic to the usual cross product on , but Layra says he has done that calculation.
Here’s the cool part: this second approach defines the 7d cross product as a kind of ‘cube’ of the 3d cross product! That came as a big surprise to me.
Here’s how it works.
Let be the space of homogeneous degree-3 polynomials on our 3d inner product space . This gets an inner product from , so let
be the orthogonal projection onto the subspace of harmonic homogeneous degree-3 polynomials. If we pick an orientation on , we can define the usual 3d cross product
using the right-hand rule.
Then Schwahn defines a bilinear operation
in a cunning way. First, note that we can cube any element and get an element . Then, let
for all . It would take work to show that there exists a unique bilinear operation obeying this formula. I haven’t done all this work. But for uniqueness, it’s enough to note that any degree-3 polynomial on is a linear combination of cubes, which follows from the ‘polarization identity’ for cubic maps.
Next Schwahn defines a cross product on by
for all .
With this definition, it’s obvious that this cross product
is -invariant. The work comes when we try to choose an isomorphism that carries this cross product to the usual cross product of imaginary octonions! And currently this seems to require a hard computation.
An alternative approach would be to check that this cross product on , together with the inner product on , obeys the axioms of a vector product algebra:
The first one is obvious because is already antisymmetric… but I haven’t figured out how to show the next two!

Re: 3d Rotations and the 7d Cross Product (Part 2)
The first and second axiom for vector cross products together amount to the trilinear form
being a 3-form, i.e. completely antisymmetric. In our case this trilinear form is given (perhaps up to some scalar factor in the choice of inner product on SymV) by the restriction of
to - and here we see easily the antisymmetry in all 3 arguments.
About the third axiom, I’m also not sure how to prove it directly, and I’m guessing for my operation it holds only up to some yet to be determined scalar factor. Since it is equivalent to the restriction
being orthogonal, it should be possible to find this scalar factor by plugging in two orthogonal vectors in and comparing lengths.
I’m currently still trying to weed out the errors in my calculations, but will report back when I’m done!