Modular Curves and Monstrous Moonshine
Posted by John Baez
Recently James Dolan and I have been playing around with modular curves — more specifically the curves and , which I’ll explain below. Monstrous Moonshine says that when is prime, the curve has genus zero iff divides the order of the Monster group, namely
Just for fun we’ve been looking at , among other cases. We used dessins d’enfant to draw a picture of , which seems to have genus , so for to have genus zero it seems we want the picture for to have a visible two-fold symmetry. After all, the torus is a two-fold branched cover of the sphere, as shown by Greg Egan here:
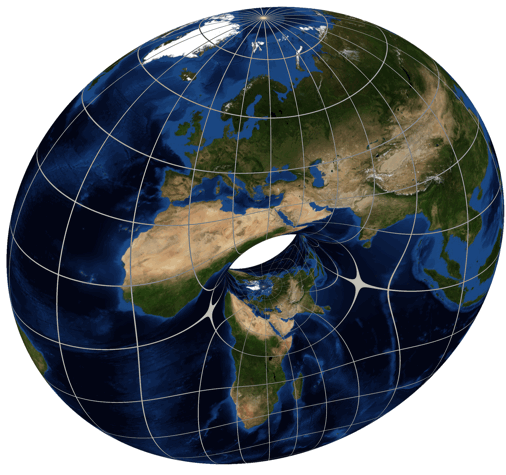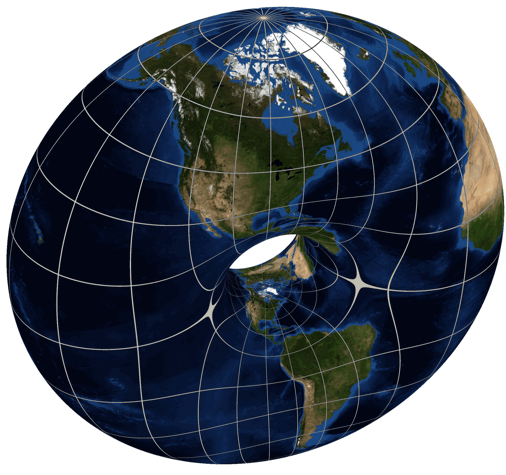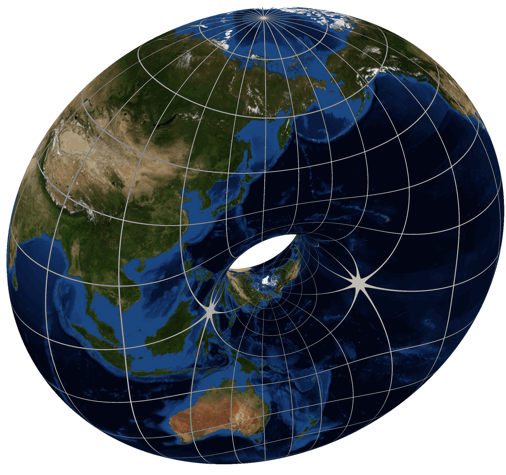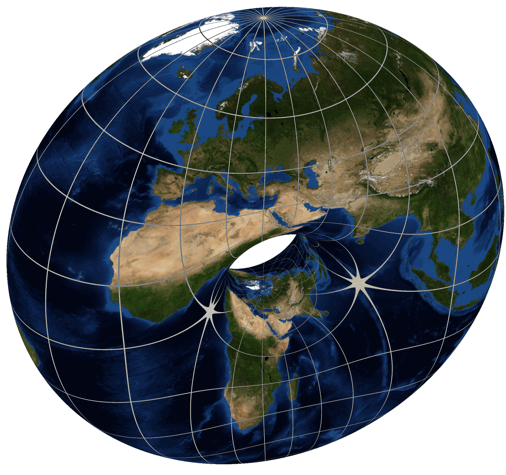
But we’re not seeing that two-fold symmetry. So maybe we’re making some mistake!
Maybe you can help us, or maybe you’d just like a quick explanation of what we’re messing around with.
To get the modular curve , we start with the quotient space
where is the complex upper half-plane and the discrete group
acts on the upper half-plane by Möbius transformations
This is the moduli space of elliptic curves with some extra structure. As a Lie group an elliptic curve is just a torus, so it has a group of -torsion points that looks like
Thus, we can equip any elliptic curve with a subgroup of its -torsion points that’s isomorphic to , in various possible ways — and that’s the extra structure I’m talking about!
Then, to form we compactify by adding finitely many extra points.
I wish I had the energy to explain how you can draw these modular curves as triangulated surfaces using a trick Grothendieck came up with, called dessins d’enfant. It is really quite childish and fun, but it’s only easy to explain using lots of pictures, and I don’t have the time to draw those. The best I can do is refer you to a series of nice posts here on the -Café, starting here:
- Tim Silverman, Pictures of modular curves (I).
and perhaps ending here:
- Tim Silverman, Pictures of modular curves (XI).
though this post declared itself the “antepenultimate”, so we may still get two more out of Tim someday!
Anyway, the normalizer of in is a slightly bigger discrete subgroup called . We can compactify
by adding finitely many extra points, and we get another modular curve, called .
is a kind of quotient of . More precisely, I think there’s a branched covering
And James and I think this should arise by taking the dessin for and modding out by some symmetries.
We’re thinking about examples. When , it seems has genus 1, and people tell us that has genus 0. So we’re hoping to find a visible two-fold symmetry of the dessin for , such that when we mod out by it we get a curve of genus zero. Can you help?
Well, I just cheated a bit and discovered that this symmetry should be the ‘Fricke involution’:
- Wikipedia, Supersingular prime (moonshine theory).
But I bet there’s a way to get a lot of visual intuition for this symmetry using dessins and other tricks.
This paper might help if you want to see more details about :
- Tom Weston, The modular curves and .
This paper about the group is probably related. but I’m not completely sure how:
- Bertram Kostant, The graph of the truncated icosahedron and the last letter of Galois, Notices of the American Mathematical Society 42 (1995), 959–968.

Re: Modular Curves and Monstrous Moonshine
I had a go at making a picture of . The edges are labelled with elements of the projective line over the field of order 11, and the opposite boundaries are identified so this lies on a torus. The green points are the (two) cusps.
I also asked James Dolan about this, and he is suggesting that is the normalizer of in SL not SL. So the Fricke involution is a bit more tricky than just finding a symmetry of this diagram.