The n-Category Café

Introduction

With the rise of the internet, numerous applications have been developed to work in a distributed way, meaning that their components (or programs) are distributed across remote servers for reasons such as convenience, efficiency, and reliability. These applications range from servicing simple commands like an end-user’s request to their smart home system to make a fresh cup of coffee or to feed their cat, to heavy computations performed by companies using cloud computing (e.g. using statistical methods to evaluate which customers are likely to change over to a competitor). Users of these services expect them to be dependable and resilient so reliability is especially important. Programs running on distributed systems are prone to, if designed incorrectly, errors that arise from faulty communication between systems (i.e. concurrency errors, which we will expound on later). The importance of designing such programs to be free of these errors becomes strikingly obvious when considering remote applications in medics or finance.

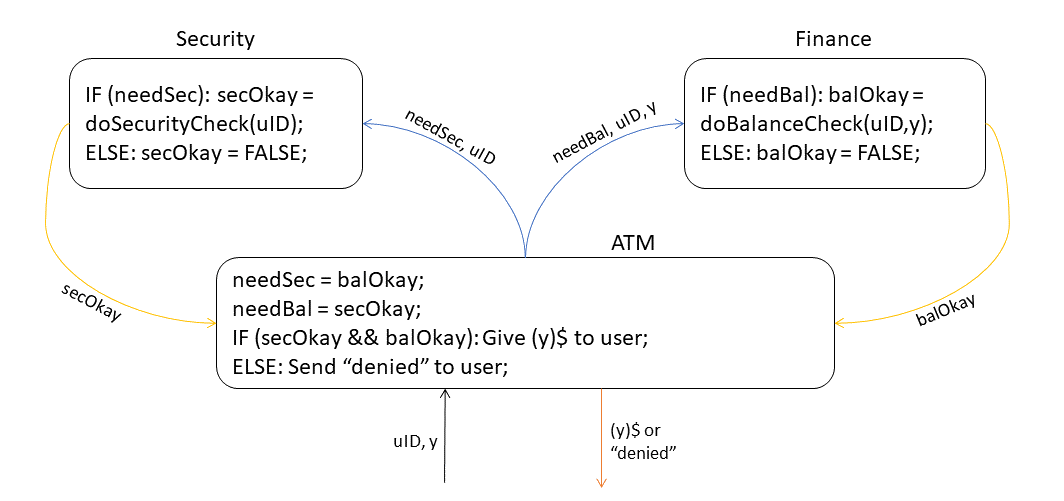
To provide an example of how things can fail, let’s consider an implementation of an ATM interacting with the following programs: Security and Finance. After a user identifies themselves, the ATM needs to know if the balance of the user’s account allows the withdrawal of the requested amount $y$ and if there were some security problems (e.g. the user’s withdrawal request was actually a theft attempt). To save work, Security only checks the user’s data bank entry if it is really needed, i.e. when the user has at least $y$ dollars in their account. Similarly, the program Finance checks the account of the user only if necessary, i.e. if Security allows a withdrawal in the first place. This implementation results in something called a deadlock, where both programs wait for a signal from the other in order to check their data about the user required to give the other the signal to proceed. In this scenario, neither process can continue.

For illustrative purposes, we’ve chosen a simple scenario but in reality distributed systems are often large and complicated. Communication errors such as the ones in the example above are often overlooked as the logic between servers becomes more complex. A formal framework for designing programs where these types of errors cannot occur has significant implications and is the topic of this blog post.

Structure of this post

In the remainder of this post, we will first explain concurrency and its possible pitfalls in slightly more detail. Afterwards, we briefly present the Curry-Howard-Lambek Isomorphism which motivated central aspects of the work this blog post is based on: The Logic of Message Passing [CP07] by Cockett and Pastro, which introduces a method to formalize concurrency. In the main section, we review their definition of a linear actegory, which provide the categorical semantics for the logic of message passing and give some intuition on how this definition relates to concurrent programs. We end this blog post with our conclusions about the paper and its implications for concurrent programs.

Preliminaries

Concurrency

How do we design programs like the ones in our example above in such a way that they never error? The answer is: providing a formal framework for concurrency. Concurrency is the process of executing programs at the same time, in non-sequential order, with no effect on the programs’ outcome. A real world example of concurrency can be observed at a restaurant where 2 chefs, for example, cook multiple orders. They are not necessarily tackling these orders in the order that they were placed, and not at the same time, yet the outcome remains (hopefully) the same. As with chefs in a kitchen, concurrency requires high levels of communication and coordination in order to work as desired.

In the domain of technology, concurrency is not solely a property of one type of system (e.g. computer networks) but of many diverse systems, so it is useful to abstract its core behaviour using category theory.

Need for formalization of concurrency

To expound on the issues that can arise in concurrent programs, we’ll first talk about deadlocks. Deadlocks occur when, as in our ATM example, two processes are waiting on a resource from another process that is waiting on another process to release a resource, and so on. A good example of this is Djikstra’s famous Dining Philosophers problem. In the problem, 5 philosophers are seated around a table and must eat pasta with two forks (left and right). The philosophers cannot eat and think at the same time, and a philosopher can only eat when each of their neighbors is thinking (and thus, is not using either fork needed by the philosopher on each side). One can imagine that the simplest implementation of this scenario would result in a philosopher unable to eat at any given time, which is the quintessential example of a deadlock.

Another error common in concurrent programs is called a livelock. A livelock occurs when processes recover from being blocked only to block eachother continuously. In the Dining Philosophers problem, a livelock would occur if all philosophers picked up one of their forks simultaneously only to then set down the forks several minutes later. No one at the table would be able to proceed despite all of the philosophers being able to pick up and put down their forks.

Both of these errors can be avoided through intelligent design of concurrent programs, but as noted earlier, preventing concurrency issues in large and complex distributed systems is an increasingly difficult problem.

The Curry-Howard-Lambek isomorphism

The Curry-Howard-Lambek (CHL) Correspondence shows an isomorphism between types, logical propositions, and Cartesian-closed categories. Take for example the proposition $\Gamma \vdash \alpha$. CHL’s correspondence shows us that we can prove this proposition by creating a program in the typed $\lambda$-calculus containing types of $\Gamma$ that returns an object of type $\alpha$ [Sub11]. The CHL correspondence began with this intuitionistic logical representation of programs and types as theorems and proofs which then allowed for the establishment of a categorical semantic equivalence. In other words, formulas were proven to be logically equivalent to objects in Cartesian-closed category $C$ and proofs were found to be equivalent to morphisms in $C$. This equivalence led to the correspondence that types belonging to $\lambda$-calculus are equivalent to objects in $C$ and terms are equivalent to morphisms in $C$. (cite resource shared by Rose) The significance of this correspondence is that we now have a paradigm for ensuring type safety (put simply: a program declared to return a certain type, returns that type) in computational programs and categorical semantics that allow us to flexibly extend the logic of the formal framework underlying this paradigm. Type errors that violate safety prevent computational programs from hanging indefinitely and allows types to be preserved throughout the execution of the program. The existence of the Curry-Howard-Lambek Isomorphism has provided modern computing with a more complete logical framework preventing programmer errors.

The Logic of Message Passing

In the paper The Logic of Message Passing [CP07], Cockett and Pastro (CP) provide a three-way equivalence between the proof theory, term calculus and the categorical semantics for concurrent programs. You can think of it as providing a CHL-esque kind of isomorphism for concurrent programs. In this blog, we will only focus on the categorical semantics part of it, which is given by a linear actegory. We won’t attempt to give the full formal definition of linear actegory, which has more than a dozen natural isomorphisms and transformations (with their associated symmetries) and various coherence conditions, but will only content ourselves with a discussion on some interesting points about it.

CP models message passing using an integrated two-tier logic. There is a logic for the messages, which you can think of as coming from the results of sequential computations. Then there is a logic of message passing, built on top of the logic of messages, which deals with the channels of communication. This distinction between the two layers is necessary for two good reasons. One is the inherent complexity of logic at both layers. But more importantly, there is a significant interaction between the two layers, where the content of the messages itself may determine the flow of the communication. Thus, it seems only wise to first separate the two layers and then capture their interaction.

Now in [CP07], the categorical semantics for the logic of messages is given by a Symmetric Monoidal Category (SMC), and the semantics for message passing is given by a Linearly Distributive category (LDC). A (symmetric) linear actegory captures the notion of a (symmetric) monoidal category acting on the LDC. This setup results in an adjunction. More formally,

Definition 3.1-Linear actegories [CP07]: Let $\mathbb{A} = (A, \ast, I, a^\ast, l^\ast, r^\ast, c^\ast)$ be a symmetric monoidal category. A symmetric linear $\mathbb{A}$-actegory consists of the following data:

• A symmetric linearly distributive category $\mathbb{X}$,
• Functors $\circ: \mathbb{A} \times \mathbb{X} \to \mathbb{X}$ and $\bullet: \mathbb{A}^\text{op} \times \mathbb{X} \to \mathbb{X}$, such that $\circ$ is the parameterized left adjoint of $\bullet$, i.e., for all $A \in \mathbb{A}$, $A\circ - \dashv A \bullet -$. The unit and counit of this adjunction are $n_{A,X}: X \to A \bullet (A\circ X)$ and $e_{A,X}: A\circ (A \bullet X) \to X$. respectively.

The adjunction in the definition of the linear actegory above captures the inherent polarity in message passing through a communication channel. Explicitly, consider the following simplified example of a bank ATM. You can think of the user and the bank as two nodes sharing a communication channel. The user and the bank end will have certain processes attached to them, and they will also need to communicate with each other for the transaction to be completed. For example, the user will have to put in her security pin $z$, and request for money $y$, while the bank will have to check against their database if the user’s request is valid or not, depending upon whether the security pin is correct, and if the amount $y$ doesn’t exceed the user’s bank balance. Now what the adjunction captures is that if the user sends a message on her right to the bank, say, her security pin $z$ and the requested amount $y$, then the bank will receive that message on its left, and if the bank sends a message on its left, say, request approved or denied, then the user will receive that message on her right-hand side. It is worth stressing that the adjunction in the definition captures the polarity in the abstract. It is only when you use this to model concurrency and you fix two nodes of the communication channel, with one on the left, and the other on the right, that you can interpret $'\circ'$ as send and $'\bullet'$ as receive. The important point, though, is not the individual meaning of $'\circ'$ and $'\bullet'$, but only the polarity relation they share.

The unit of this adjunction formally captures the idea that someone, say, Alice, sending and then receiving a message of the type $A$ is the same as Alice just forwarding (or doing nothing to) the message, hence the name unit.

There are a lot of natural isomorphisms and natural transformations in the data of the definition of linear actegory. We won’t list all of them, but will look at a few interesting ones.

• We have that, for $I \in \mathbb{A}$ and for all $X \in \mathbb{X}$, $u_\circ: I \circ X \to X$ and $u_\bullet: X \to I \bullet X$ are natural isomorphisms in $\mathbb{X}$. In English, it means that Alice sending (resp. receiving) an instance of the empty message type is the same as Alice sending (resp. receiving) no message at all.
• We also have that, for all $A,B \in \mathbb{A}$ and $X \in \mathbb{X}$, $a_{\circ}^{\ast}: (A \ast B) \circ X \to A \circ (B \circ X)$ and $a_{\bullet}^{\ast} : A\bullet (B\bullet X) \to (A \ast B)\bullet X$, as natural isomorphisms in $\mathbb{X}$. In English, this says that Alice sending (resp. receiving) two consecutive messages of type $A$ and (then) $B$ is the same as Alice sending (resp. receiving) a message of type $(A\ast B)$.

• There are also many natural transformations in the data of the definition of a linear actegory. We will just highlight one, which hints at the causal structure in the logic of message passing. We have that, for any $A, B \in \mathbb{A}$ and $X \in \mathbb{X}$, $d_{\bullet}^{\circ}: A \circ (B \bullet X) \to B \bullet (A \circ X)$ is a natural transformation in $\mathbb{X}$. The important thing, however, is that this is only a natural transformation, not a natural isomorphism. This means that if Alice sends some resource first ($B$) before she is receives any ($A$), then she might as well receive $A$ first before she sends $B$. But if she is receives $A$ first before she sends $B$, then she can’t always choose to do the opposite, as $B$ might causally depend on $A$. This (natural) transformation hints at the causal structure in the logic of message passing. It is also highlighted in Chad Nester’s paper [[Nes23]](https://arxiv.org/abs/2010.08233), which presents a more degenerate model of message passing.

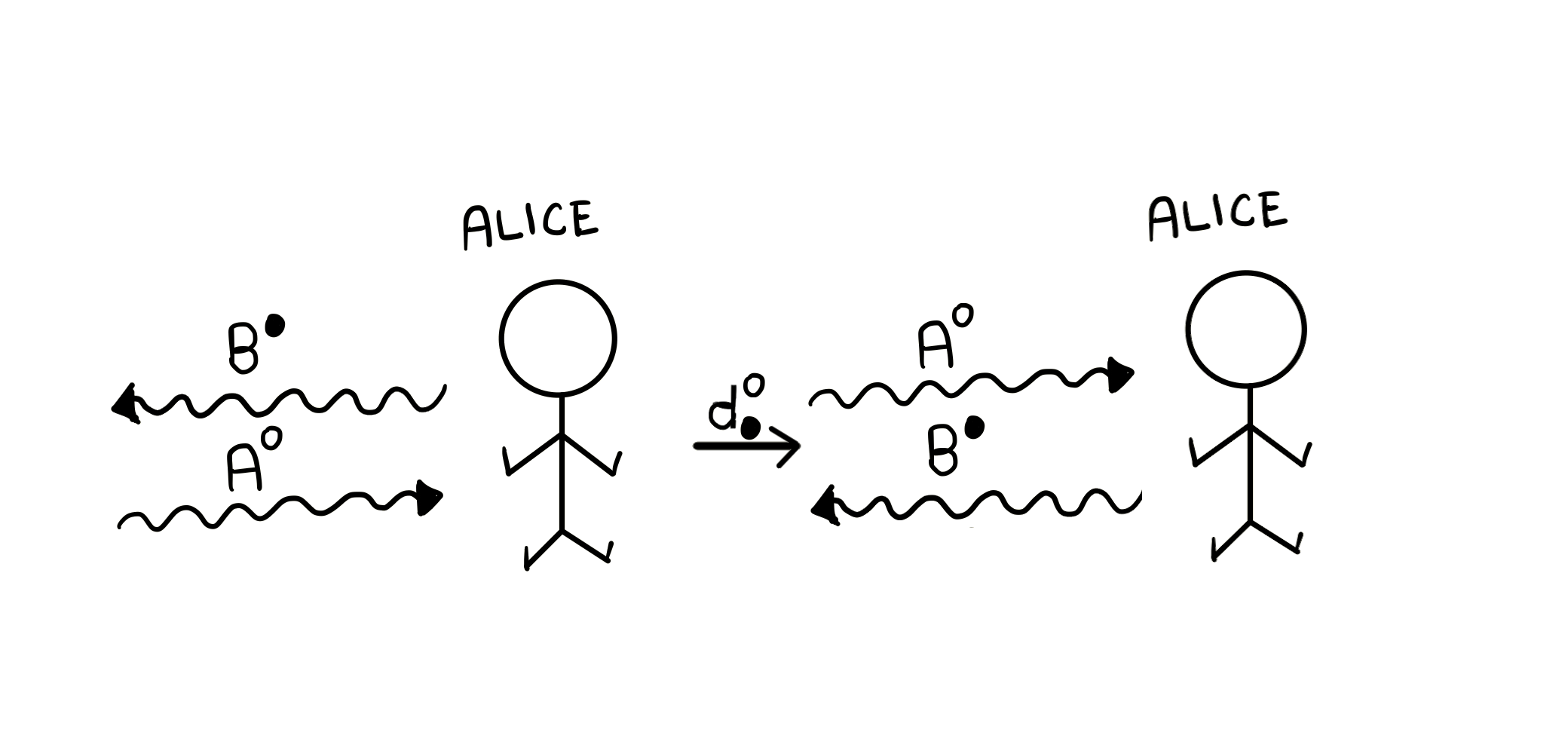
• Finally, there is a lot of symmetry in the data, coming from the symmetry of tensor and par of the LDC $\mathbb{X}$, they symmetry of $\ast$ of the SMC $\mathbb{X}$, and their various combinations. The notion of a linear $\mathbb{A}$-actegory is preserved under these symmetries. This data is also subjected to various coherence conditions (27 of them, for a full list see [[CP07]](https://arxiv.org/abs/math/0703713)), which takes care that nothing goes wrong when various kinds of morphisms interact with one another.

Conclusion and open questions

The most significant advantage of [CP07] is the generality in which it captures concurrency. It allows for creating a programming language which by design prevents errors that arise in concurrent programs such as deadlocks and livelocks. This generality comes at the cost of complexity. Indeed, it is very complicated to utilize the results of this paper; formalising concurrency remains hard to do and is an active field of research. Nevertheless, other works as [Nes23] refer back to it and show how degenerate versions of linear actegories can describe concurrency, although no logic and programming syntax is given. This raises the question if there is any situation where one needs the full generality of linear actegories. Although we can not give a definite answer to it, there is a hint that it might be needed to formalise the concurrency of quantum computing with infinite dimensionality. Expressing infinite-dimensional quantum computing in category theory is itself an open problem, but there is work suggesting to use linear distributive categories for it [CSS21].

References

[CP07] J. R. B. Cockett and Craig Pastro (2007). The logic of message passing. arXiv: math/0703713 [math.CT].

[Sub11] Subashis Chakraborty (2011). Curry-Howard-Lambek Correspondence. Online resource

[Nes23] Chad Nester (2023). Concurrent Process Histories and Resource Transducers. arXiv: 2010.08233 [cs.LO].

[CSS21] J.R.B. Cockett and Cole Comfort and Priyaa Srinivasan (2021). Dagger linear logic for categorical quantum mechanics. arXiv: 1809.00275 [math.CT].