Why Category Theory Matters
Posted by John Baez
No, I’m not going to tell you why category theory matters. To learn that, you must go here:
- Robb Seaton, Why category theory matters, rs.io.
It’s interesting to see an outsider’s answer to this subject. He starts with a graph purporting to show the number of times — per year, I guess? — that the phrase “category theory” has been mentioned in books:
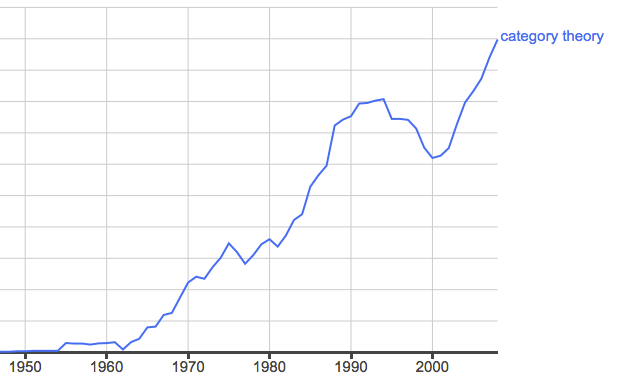
I’m curious about the plunge after 1990. I hadn’t noticed that.
I’m amused and flattered, but also a bit unnerved to read that
Generally speaking, there seems to be a cabal of radical category theorists, led by John Baez, who are reinterpreting anything interesting in category theoretic terms.
Of course it’s meant to be humorous. The unnerving part is the idea that I’m “leading” anybody — except perhaps my grad students. It seems to me rather that category theory has an inherent tendency to spread its reach, and I’m just one of a large group of people who have tuned in to this.

Re: Why Category Theory Matters
My first guess about the drop-off is rather morbid: it’s the time around which the people who founded category theory started passing away. It took a little while perhaps for the next generation of people to pick up the slack after the intermediate generations were a little jaded by the enthusiasm of category theorists of the 1970s. Or perhaps we got satisfied with existing textbooks. Categories for the Working Mathematician, Topos Theory, Sheaves in Geometry and Logic, and Toposes Triples and Theories, for instance, cast long shadows. Then The Elephant got published at the turn of the century, and slowly people have been writing books again.
Or maybe people really just took up the internet in a serious way, and relied less on the paper medium? TAC got up and running at the time of that peak just before the big dip.