SageMath and 3D Models in Webpages
Posted by Simon Willerton
I want to write a few posts (which means at least one!) on things I’ve done around SageMath, not necessarily about SageMath, but using that as a springboard. Here I’ll say how I used it to help visualization – for both the students and me! – in the differential geometry course I’ve been teaching this semester.
SageMath (formerly SAGE) is a computer algebra system like Mathematica, Maple and MATLAB. However, unlike those other systems, it doesn’t start with an ‘M’. More importantly though, it is an open source project which, amongst other things, provides a unified ‘front-end’ for many other pieces of open source mathematical software such as Maxima, PARI and GAP. Having been using Maple since I was a PhD student, I started to make the switch to SageMath a couple of years ago, which was not that easy as the biggest problem with SageMath is the lack of introductory material and documentation, although this is now definitely improving, see for instance the book Mathematical Computation with SageMath, originally available in French.
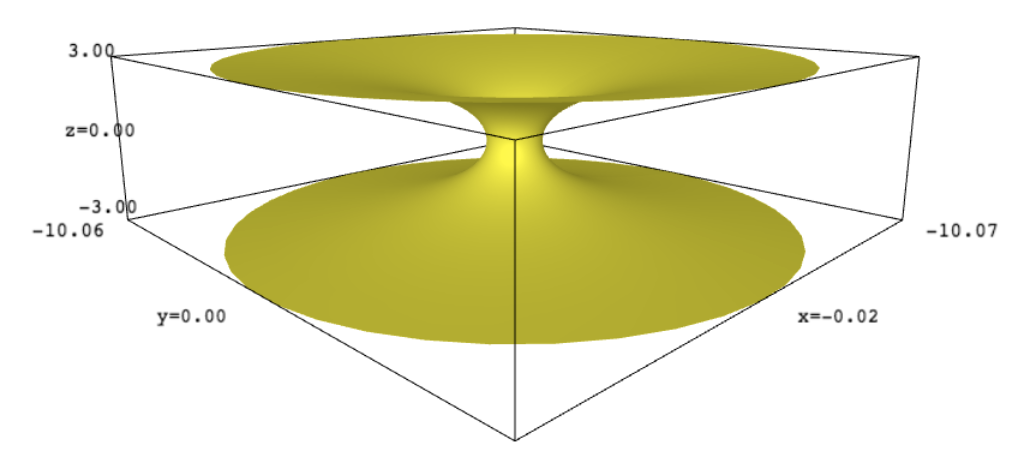
Now onto visualization, here is a static picture of a catenoid surface.
Beneath the fold I’ll explain two ways in which you can use SageMath to embed a rotatable model of the surface in a webpage. All being well, in the main body of the post you should be able to play with the catenoid yourself.
This is, in some sense, a follow-on from one of the first posts I wrote here on using blender for creating 3d models of surface diagrams, nearly eight years ago.
I want to mention two ways to get 3d models into web pages using SageMath. One is by actually including some SageMath on the page which the user can even alter and the other is by including the output of SageMath that you need to alter a little. I won’t go into too much ‘how-to’ detail. I can answer any questions of that nature in the comments.
Using SageCell
SageMathCell is a wonderful thing that allows you to have SageMath running inside a webpage; well, actually it runs on a server in the Mathematics Department at the Universidad Autónoma de Madrid, but the output is displayed on your webpage. It’s very easy to set-up and just requires you to cut and paste some javacript into your webpage’s html. Unfortunately, the anti-hacking security measures here at the Café mean that I can’t do it on this webpage but I can send you over to my page where you can try it yourself.
Click on any of the evaluate buttons to get the surface and then you can use your mouse/trackpad/whatever to move the surface around. I would recommend going down the catenoid or helicoid for something a bit more interesting.
You can then edit the SageMath and hit ‘Evaluate’ again to change the surface. Change the ‘cosh’ in the catenoid to a ‘cos’ and see what happens!
This approach allows the students some freedom to experiment with the SageMath code, if they like, without having to actual learn SageMath or to install on their own machines or to register for the cloud version of SageMath, CoCalc (formerly SageMathCloud). If they like what they see then they can move in that direction.
Exporting to html from a Jupyter notebook
An alternative approach is to generate the 3d graphics yourself and then just include the output in the webpage. The way I’ve done this is to use ‘Download as HTML’ in a Jupyter notebook. If you then look in the .html file you’ll see a another .html file inside which encodes the 3d model. You can extract this and either copy the code to your own html or include it as an iframe or object. I can give more details if anyone wants them, or maybe someone can suggest a more efficient workflow.
Anyway, here’s the kind of result you can get. You should be able to move it around with your mouse!
I will just finish with the following little treat for John.

Re: SageMath and 3D Models in Webpages
You should have explicitly mentioned that your last graphic is dynamic and people should drag their mouse cursor over it. That this might happen does not seem a possibility unless one has gone off to play with the earlier examples. From inspection this is achieved with an
<object>that includes a separate .html file.