The Origin of the Word “Quandle”
Posted by John Baez
A quandle is a set equipped with a binary operation with number of properties, the most important being that it distributes over itself:
They show up in knot theory, where the operation describes what happens when one strand crosses over another… and the laws are chosen so that the quandle gives an invariant of a knot, independent of how you draw it. Even better, the quandle is a complete invariant of knots: if two knots have isomorphic quandles, there’s a diffeomorphism of mapping one knot to the other.
I’ve always wondered where the name ‘quandle’ came from. So I decided to ask their inventor, David Joyce—who also proved the theorem I just mentioned.
He replied:
I needed a usable word. “Distributive algebra” had too many syllables. Piffle was already taken. I tried trindle and quagle, but they didn’t seem right, so I went with quandle.
So there you go! Another mystery unraveled.
Actually, it turns out my former student Alissa Crans had already asked him this question, and he’d given another answer:
I wanted a short term, just one word, that wasn’t taken. I didn’t want to use a common word like group or ring which had a meaning in common English, so I selected a nonsense word. It just sounded good. I was thinking at the time that an alternative would be “conjugacy algebra,” but that was too long, and the word “algebra” suggests that addition and multiplication should be operations, which they aren’t in quandles.
Taken together, I hope they add up to the whole story.

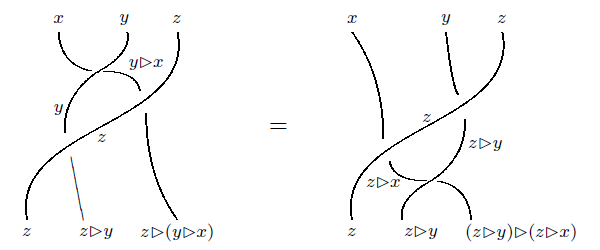
Re: The Origin of the Word “Quandle”
Cool! In a completely different setting there are operations which behave similarly (they distribute over themselves): weakening and substitution in type theory!
Taking an algebraic point of view of what type dependency is, one could model contexts as the objects of a category , and families as the morphisms. And then there is a weakening structure which consists of functors for any morphism , such that
for any , and .
This is just a way of saying that weakening distributes over itself, and I also think of it as saying that each preserves the weakening structure (on ). Forgetting about all the rest of the structure of type dependency, there is thus a notion of weakening system (which is a category with weakening structure), satisfying the same kind of distributivity as a quandle. And groups with conjugation form an example of such weakening systems.