The Tenfold Way (Part 3)
Posted by John Baez
My last article on the ten-fold way was a piece of research in progress — it only reached a nice final form in the comments. Since that made it rather hard to follow, let me try to present a more detailed and self-contained treatment here!
But if you’re in a hurry, you can click on this:
and get my poster for next week’s scientific advisory board meeting at the Centre for Quantum Technologies, in Singapore. That’s where I work in the summer, and this poster is supposed to be a terse introduction to the ten-fold way.
First we’ll introduce the ‘Brauer monoid’ of a field. This is a way of assembling all simple algebras over that field into a monoid: a set with an associative product and unit. One reason for doing this is that in quantum physics, physical systems are described by vector spaces that are representations of certain ‘algebras of observables’, which are sometimes simple (in the technical sense). Combining physical systems involves taking the tensor product of their vector spaces and also these simple algebras. This gives the multiplication in the Brauer monoid.
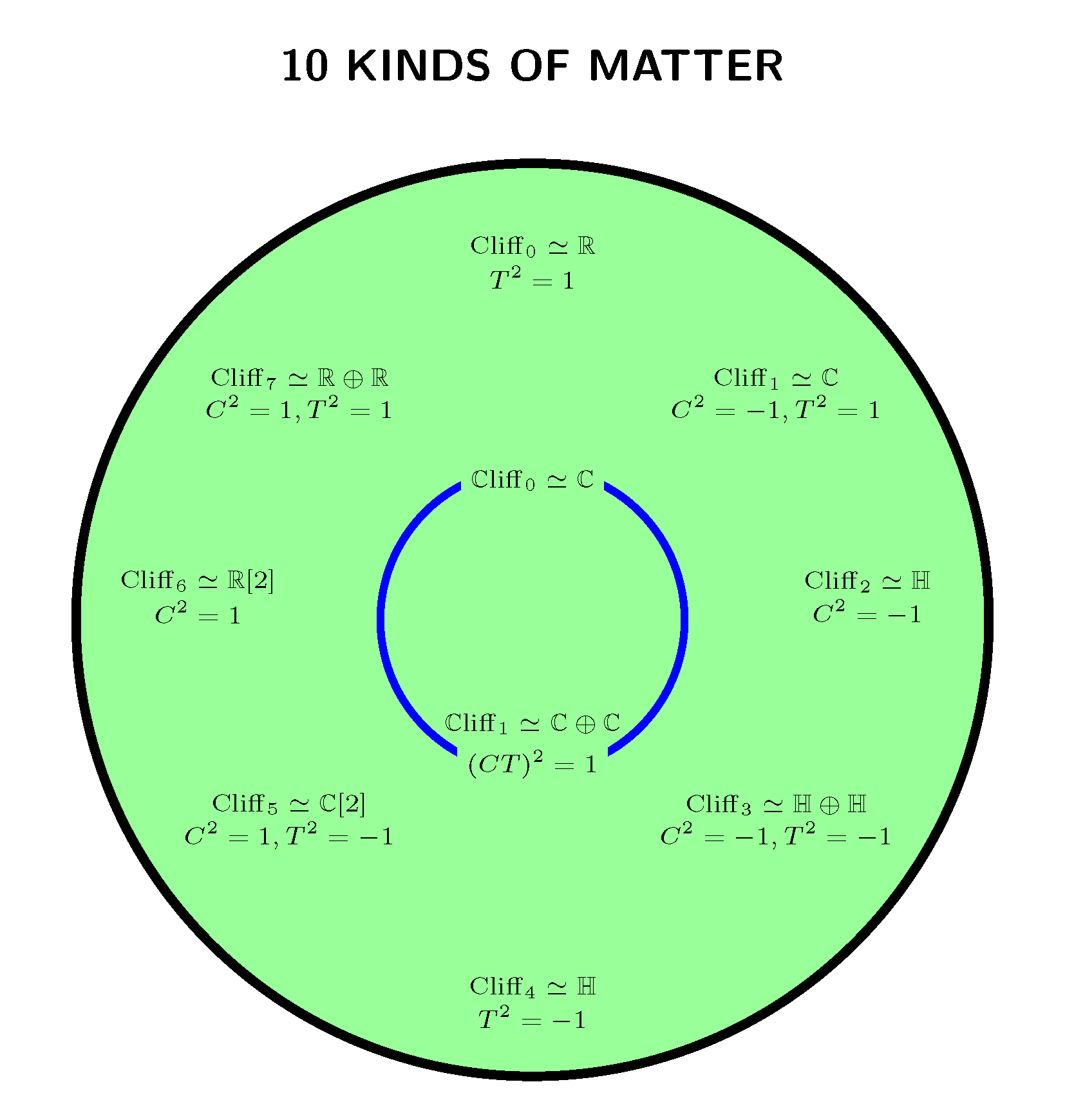
We then turn to a larger structure called the ‘super Brauer monoid’ or ‘Brauer–Wall monoid’. This is the ‘super’ or -graded version of the same idea, which shows up naturally in physical systems containing both bosons and fermions. For the field , the super Brauer monoid has 10 elements. This gives a nice encapsulation of the ‘ten-fold way’ introduced in work on condensed matter physics. At the end I’ll talk about this particular example in more detail.
Actually elements of the Brauer monoid of a field are equivalence classes of simple algebras over this field. Thus, I’ll start by reminding you about simple algebras and the notion of equivalence we need, called ‘Morita equivalence’. Briefly, two algebras are Morita equivalent if they have the same category of representations. Since in quantum physics it’s the representations of an algebra that matter, this is sometimes the right concept of equivalence, even though it’s coarser than isomorphism.
Review of algebra
We begin with some material that algebraists consider well-known.
Simple algebras and division algebras
Let be a field.
By an algebra over we will always mean a finite-dimensional associative unital -algebra: that is, a finite-dimensional vector space over with an associative bilinear multiplication and a multiplicative unit .
An algebra over is simple if its only two-sided ideals are and itself.
A division algebra over is an algebra such that if there exists such that . Using finite-dimensionality the following condition is equivalent: if and then either or .
A division algebra is automatically simple. More interestingly, by a theorem of Wedderburn, every simple algebra over is an algebra of matrices with entries in some division algebra over . We write this as
where is our shorthand for the algebra of matrices with entries in .
The center of an algebra over always includes a copy of , the scalar multiples of . If is a division algebra, its center is a commutative algebra that’s a division algebra in its own right. So is field, and it’s a finite extension of , meaning it contains as a subfield and is a finite-dimensional algebra over .
If is a simple algebra over , its center is isomorphic to the center of some , which is just the center of . So, the center of is a field that’s a finite extension of . We’ll need this fact when defining in the multiplication in the Brauer monoid.
Example. I’m mainly interested in the case . A theorem of Frobenius says the only division algebras over are itself, the complex numbers and the quaternions . Of these, the first two are fields, while the third is noncommutative. So, the simple algebras over are the matrix algebras , and . The center of and is , while the center of is , the only nontrivial finite extension of .
Example. The case is more boring, because is algebraically closed. Any division algebra over an algebraically closed field must be itself. (To see this, consider and look at the smallest subring of containing and and closed under taking inverses. This is a finite hence algebraic extension of , so it must be .) So if is algebraically closed, the only simple algebras over are the matrix algebras .
Example. The case where is a finite field has a very different flavor. A theorem of Wedderburn and Dickson implies that any division algebra over a finite field is a field, indeed a finite extension of . So, the only simple algebras over are the matrix algebras where is a finite extension of . Moreover, we can completely understand these finite extensions, since the finite fields are all of the form where is a prime and , and the only finite extensions of are the fields where divides .
Morita equivalence and the Brauer group
Given an algebra over we define to be the category of left -modules. We say two algebras over are Morita equivalent if . In this situation we write .
Isomorphic algebras are Morita equivalent, but this equivalence relation is more general; for example we always have , where is the algebra of matrices with entries in .
We’ve seen that if is simple, , and this implies . On the other hand, we have . So, every simple algebra over is Morita equivalent to a division algebra over .
As a set, the Brauer monoid of will simply be the set of Morita equivalence classes of simple algebras over . By what I just said, this is also the set of Morita equivalence classes of division algebras over . The trick will be defining multiplication in the Brauer monoid. For this we need to think about tensor products of algebras.
The tensor product of two algebras over is another algebra over , which we’ll write as . This gets along with Morita equivalence:
However, the tensor product of simple algebras need not be simple! And the tensor product of division algebras need not be a division algebra, or even simple. So, we have to be a bit careful if we want a workable multiplication in the Brauer monoid.
For example, take . The division algebras over are and the quaternions . We have
so this particular tensor product of division algebras over is simple and thus Morita equivalent to another division algebra over . On the other hand,
and this is not a division algebra, nor even simple, nor even Morita equivalent to a simple algebra.
What’s the problem with the latter example? The problem turns out to be that the division algebra does not have as its center: it has a larger field, namely itself, as its center.
It turns out that if you tensor two simple algebras over a field and they both have just as their center, the result is again simple. So, in Brauer theory, people restrict attention to simple algebras over having just as their center. These are called central simple algebras over . The set of Morita equivalence classes of these is closed under tensor product, so it becomes a monoid. And this monoid happens to be be an abelian group: Brauer group of , denoted . I want to work with all simple algebras over . So I will need to change this recipe a bit. But it will still be good to compute a few Brauer groups.
To do this, it pays to note that element of has a representative that is a division algebra over whose center is . Why? Every simple algebra over is for some division algebra over . is central simple over iff the center of is , and is Morita equivalent to . Using this, we easily see:
Example. The Brauer group is , the 2-element group consisting of and . We have
Example. The Brauer group of any algebraically closed field is trivial, since the only division algebra over is itself. Thus .
Example. The Brauer group of any finite field is trivial, since the only division algebras over are fields that are finite extensions of , and of these only itself has as center.
Example. Just so you don’t get the impression that Brauer groups tend to be boring, consider the Brauer group of the rational numbers:
where the sum is over all primes. This is a consequence of the Albert–Brauer–Hasse–Noether theorem. The funny-looking is just a way to think about the group as a subgroup of . The elements of this correspond to itself and a rational version of the quaternions. The other stuff comes from studying the situation ‘locally’ one prime at a time. However, the two aspects interact.
The Brauer monoid of a field
Let be a field and its algebraic completion. Let be the set of intermediate fields
where is a finite extension of . This set is partially ordered by inclusion, and in fact it is a semilattice: any finite subset of has a least upper bound. We write for the least upper bound of . This is just the smallest subfield of containing both and .
We define the Brauer monoid of to be the disjoint union
So, every simple algebra over shows up in here: if is a simple algebra over with center , the Morita equivalence class will appear as an element of . However, isomorphic copies of the same simple algebra will show up repeatedly in the Brauer monoid, since different field extensions of can still be isomorphic as fields.
How do we define multiplication in the Brauer monoid? The key is that the Brauer group is functorial. Suppose we have an inclusion of fields in the semilattice . Then we get a homomorphism
as follows. Any element comes from a central simple algebra over ; the algebra will be central simple over , and we define
Of course we need to check that this is well-defined, but this is well-known. People call restriction, since larger fields have smaller Brauer groups, but I’d prefer to call it ‘extension’, since we’re extending an algebra to be defined over a larger field.
It’s easy to see that if then
and this together with
implies that we have a functor
So now suppose we have two elements of and we want to multiply them. To do this, we simply write them as and , map them both into , and then multiply them there:
This can also be expressed with less jargon as follows:
However, the functorial approach gives a nice outlook on this basic result:
Proposition. With the above multiplication, is a commutative monoid.
Proof. The multiplicative identity is , and commutativity is obvious, so the only thing to check is associativity. This is easy enough to do directly, but it’s a bit enlightening to notice that it’s a special case of an idea that goes back to A. H. Clifford.
In modern language: suppose we have any semilattice and any functor . This gives an abelian group for any , and a homomorphism
whenever . Then the disjoint union
becomes a commutative monoid if we define the product of and by
Checking associativity is an easy fun calculation, so I won’t deprive you of the pleasure. Moreover, there’s nothing special about abelian groups here: a functor from to commutative monoids would work just as well. ∎
Let’s see a couple of examples:
Example. The Brauer monoid of the real numbers is the disjoint union
This has three elements: , and . Leaving out the brackets, the multiplication table is
So, this monoid is isomorphic to the multiplicative monoid . This formalizes the multiplicative aspect of Dyson’s ‘threefold way’, which I started grappling with in my paper Division algebras and quantum theory. If you read that paper you can see why I care: Hilbert spaces over the real numbers, complex numbers and quaternions are all important in quantum theory, so they must fit into a single structure. The Brauer monoid is a nice way to describe this structure.
Example. The Brauer monoid of a finite field is the disjoint union
where is the lattice of subfields of the algebraic closure that are finite extensions of . However, we’ve seen that is always the trivial group. Thus
with the monoid structure being the operation in the lattice .
Example. The Brauer monoid of seems quite complicated to me, since it’s the disjoint union of for all that are finite extensions of . Such fields are called algebraic number fields, and their Brauer groups can, I believe, be computed using the Albert–Brauer–Hasse–Noether theorem. However, here we are doing this for all algebraic number fields, and also keeping track of how they ‘fit together’ using the so-called restriction maps whenever . The absolute Galois group of a field always acts on its Brauer monoid, so the rather fearsome absolute Galois group of acts on , for whatever that’s worth.
Fleeing the siren song of number theory, let us move on to my main topic of interest, which is the ‘super’ or -graded version of this whole story.
Review of superalgebra
We now want to repeat everything we just did, systematically replacing the category of vector spaces over by the category of super vector spaces over , which are graded vector spaces:
We call the elements of even and the elements of odd. Elements of either or are called homogeneous, and we say an element has degree . A morphism in the category of super vector spaces is a linear map that preserves the degree of homogeneous elements.
The category of super vector spaces is symmetric monoidal in a way where we introduce a minus sign when we switch two odd elements.
Simple superalgebras and division superalgebras
A superalgebra is a monoid in the category of super vector spaces. In other words, it is a super vector space where the vector space is an algebra in the usual sense and
where we do our addition mod 2. There is a tensor product of superalgebras, where
and multiplication is defined on homogeneous elements by:
where are the elements getting switched.
An ideal of a superalgebra is homogeneous if it is of the form
where . We can take the quotient of a superalgebra by a homogeneous two-sided ideal and get another superalgebra. So, we say a superalgebra over is simple if its only two-sided homogeneous ideals are and itself.
A division superalgebra over is a superalgebra such that if is homogeneous then there exists such that .
At this point it is clear what we aim to do: generalize Brauer groups to this ‘super’ context by replacing division algebras with division superalgebras. Luckily this was already done a long time ago, by Wall:
• C. T. C. Wall, Graded Brauer groups, Journal für die reine und angewandte Mathematik 213 (1963–1964), 187–199.
He showed there are 10 division superalgebras over and showed how 8 of these become elements of a kind of super Brauer group for , now called the ‘Brauer–Wall’ group. The other 2 become elements of the Brauer–Wall group of . A more up-to-date treatment of some of this material can be found here:
• Pierre Deligne, Notes on spinors, in Quantum Fields and Strings: a Course for Mathematicians, vol. 1, AMS. Providence, RI, 1999, pp. 99–135.
Nontrivial results that I state without proof will come from these sources.
Every division superalgebra is simple. Conversely, we want a super-Wedderburn theorem describing simple superalgebras in terms of division superalgebras. However, this must be more complicated than the ordinary Wedderburn theorem saying every simple algebra is a matrix algebra with a division algebra.
After all, besides matrix algebras, we have ‘matrix superalgebras’ to contend with. For any let be the super vector space with even part and odd part . Then its endomorphism algebra
becomes a superalgebra in a standard way, called a matrix superalgebra. Matrix superalgebras are always simple.
Deligne gives a classification of ‘central simple’ superalgebras, and from this we can derive a super-Wedderburn theorem. But what does ‘central simple’ mean in this context?
The supercommutator of two homogeneous elements , of a superalgebra is
We can extend this by bilinearity to all elements of . We say supercommute if . The supercenter of is the set of elements in that supercommute with every element of . If all elements of supercommute, or equivalently if the supercenter of is all of , we say is supercommutative.
I believe a superalgebra over is central simple if is simple and its supercenter is just , the scalar multiples of the identity. Deligne gives a more complicated definition of ‘central simple’, but then in Remark 3.5 proves it is equivalent to being semisimple with supercenter just . I believe this is equivalent to the more reasonable-sounding condition I just gave, but have not carefully checked.
In Remark 3.5, Deligne says that by copying an argument in Chapter 8 of Bourbaki’s Algebra one can show:
Proposition. Any central simple superalgebra over is of the form for some division superalgebra whose supercenter is . Conversely, any superalgebra of this form is central simple.
Starting from this, Guo Chuan Thiang showed me how to prove the:
Super-Wedderburn Theorem. Suppose is a simple superalgebra over , where is a field not of characteristic 2. Its supercenter is purely even, and is a field extending . is isomorphic to where is some division superalgebra over .
It follows that any simple superalgebra over is of the form where is a division superalgebra over . Conversely, if is any division algebra over , then is a simple superalgebra over .
Proof. Suppose is a simple superalgebra over , and let be its supercenter. Suppose is a nonzero homogeneous element of . Then is a graded two-sided ideal of . Since this ideal contains it is nonzero. Thus, this must be itself. So, there exists such that .
If is even, must be as well, and we obtain , so has an inverse. Thus, the even part of is a field.
If is odd, it satisfies . Multiplying on the left by , then it follows that , so , since is not of characteristic 2.
In short, nonzero elements of must be even and invertible. It follows that is purely even, and is a field extending . is central over this field , so by the previous proposition we see for some division superalgebra over . will automatically be a division superalgebra over the smaller field as well.
Conversely, suppose is a division algebra over . Since is simple, its supercenter will be a field extending . By the previous proposition will be a central simple superalgebra over . It follows that is simple as a superalgebra over . ∎
Here is an all-important example:
Example. Let be the free superalgebra over on an odd generator whose square is -1. This superalgebra has a 1-dimensional even part and a 1-dimensional odd part. It is a division superalgebra. It is not supercommutative, since does not supercommute with itself. It is central simple: its supercenter is just . Over an algebraically closed field of characteristic other than 2, the only division superalgebras are itself and .
I don’t understand what happens in characteristic 2.
Morita equivalence and the Brauer–Wall group
The Brauer–Wall group consists of Morita equivalence classes of central simple superalgebras, or equivalently, Morita equivalence classes of division superalgebras. For this to make sense, first we need to define Morita equivalence.
Given a superalgebra over we define a left module to be a super vector space over equipped with a morphism (that is, a grade-preserving linear map)
obeying the usual axioms of a left module. We define a morphism of left -modules in the obvious way, and let be the category of left -modules.
We say two algebras over are Morita equivalent if . In this situation we write .
Example. Every matrix superalgebra is Morita equivalent to .
Example. If and then .
Example. Since every central simple superalgebra over is of the form for some division superalgebra whose supercenter is just , the previous two examples imply that every central simple superalgebra over is Morita equivalent to a division superalgebra whose center is just .
We define the Brauer–Wall group of the field to be the set of Morita equivalence classes of central simple superalgebras over , given the following multiplication:
This is well-defined because the tensor product of central simple superalgebras is again central simple. Given that, is clearly a commutative monoid. But in fact it’s an abelian group.
Since every central simple superalgebra over is Morita equivalent to a division superalgebra whose center is just , we can compute Brauer–Wall groups by focusing on these division superalgebras.
Example. For any algebraically closed field , the Brauer–Wall group is , where the two elements are and . In particular, is . Wall showed that this is related to the period-2 phenomenon in complex K-theory and the theory of complex Clifford algebras. The point is that
where is the complex Clifford algebra on square roots of -1, made into a superalgebra in the usual way. It is well-known that
and this gives the period-2 phenomenon.
Example. is much more interesting: by a theorem of Wall, this is . This is generated by . Wall showed that this is related to the period-8 phenomenon in real K-theory and the theory of real Clifford algebras. The point is that
where is the real Clifford algebra on square roots of -1, made into a superalgebra in the usual way. It is well-known that
and this gives the period-8 phenomenon.
Example. More generally, Wall showed that as long as doesn’t have characteristic 2, is an iterated extension of by by . For a quick modern proof, see Lemma 3.7 in Deligne’s paper. In the case all three of these groups are and the iterated extension gives .
The Brauer–Wall monoid
And now the rest practically writes itself. Let be a field and its algebraic completion. As before, let be the semilattice of intermediate fields
where is a finite extension of .
We define the underlying set of Brauer–Wall monoid of to be the disjoint union
To make this into a commutative monoid, we use the functoriality of the Brauer–Wall group. Suppose we have an inclusion of fields in the semilattice . Then we get a homomorphism
as follows:
and this gives a functor
Using this, we multiply two elements in the Brauer–Wall monoid as follows. Given and , their product is
or in other words
Proposition. With the above multiplication, is a commutative monoid.
Proof. The same argument that let us show associativity for multiplication in the Brauer monoid works again here. ∎
Example. As a set, the Brauer–Wall monoid of the real numbers is the disjoint union
The monoid operation — let’s call it addition now — is the usual addition on when applied to two elements of that group, and the usual addition on when applied to two elements of that group. The only interesting part is when we add an element and an element . For this we need to convert into an element of . For that we use the homomorphism
which sends to . More concretely,
takes an integer mod 8 and gives the corresponding integer mod 2.
So, very concretely,
where the monoid operation in is addition mod 8 for two lightface numbers, but addition mod 2 for two boldface numbers or a boldface and a lightface one.
Conclusion
I had meant to include a section explaining in detail how the 10 elements of this monoid correspond to 10 kinds of matter, but this post is getting too long. So for now, at least, you can click on this picture to get an explanation of that!
References
Besides what I’ve already mentioned about the classification of simple superalgebras, here are some other links. Wall proved a kind of super-Wedderburn theorem starting in the section of his paper called Elementary properties. Natalia Zhukavets has an Introduction to superalgebras which in Theorem 1.5 proves that in an algebraically closed field of characteristic different than 2, any simple superalgebra is of the form or where , being an odd square root of 1. Over an algebraically closed field, this superdivision algebra is isomorphic to the division algebra that I called . Over a field that is not algebraically closed, they can be different, and there can be many nonisomorphic division algebras obtained by adjoining to an odd square root of where .
Jinkui Wan and Weiqiang Wang have a paper with a Digression on superalgebras which summarizes Wall’s results in more modern language. Benjamin Gammage has an expository paper with a Classification of finite-dimensional simple superalgebras. This only classifies the ‘central’ ones — but as we’ve seen, that’s the key case.

Re: The Ten-Fold Way (Part 3)
Hi John The link for your Ten-Fold Way poster seems to be dead