Wormholes and Entanglement

January 19, 2014

Posted by John Baez

$MathML-enabled post (click for more details).$

For the last couple years, people interested in quantum gravity have been arguing about the ‘firewall problem’. It’s a thought experiment involving black holes that claims to demonstrate an inconsistency in some widely held assumptions about how quantum mechanics and general relativity fit together. Everyone is either scratching their heads over it, struggling to find a way out… or grumbling that the problem isn’t real, and everyone else has gone crazy.

While the firewall problem has roots going back earlier, the paper that got everyone interested came out in July 2012:

Ahmed Almheiri, Donald Marolf, Joseph Polchinski and James Sully, Black holes: complementarity or firewalls?

They called it the ‘firewall’ problem because one way out is to assume that when you fall into a black hole you hit a ‘wall of fire’ — a region of hot radiation — as you cross the event horizon. That sounds crazy: the equivalence principle says you shouldn’t feel anything special as you fall through the horizon, at least if the black hole is big enough. But they claimed this crazy-sounding solution was the most conservative way out!

In June of the following year, two extremely reputable physicists, in their attempts to avoid this conclusion, came up with an idea that sounds even crazier: every pair of entangled quantum particles is connected by a wormhole!

Juan Maldacena and Leonard Susskind, Cool horizons for entangled black holes.

They called their proposal EPR = ER, which is a joke referring to two papers Einstein wrote in 1935. EPR stands for ‘Einstein–Podolsky–Rosen’, the authors of a famous paper on quantum entanglement, a spooky way that distant objects can be correlated. ER stands for ‘Einstein–Rosen’, the authors of a famous paper on wormholes, solutions of general relativity in which distant regions of space can be connected by a kind of tunnel, or handle.

I haven’t been thinking much about quantum gravity lately, but the recent convulsions in my old favorite subject caught my attention. In particular, I’d long been fond of the idea that when we finally understand quantum gravity, the distinction between quantum mechanics and our theory of spacetime will evaporate. There’s a lot of evidence coming from category theory, which reveals analogies between the two:

John Baez, Quantum quandaries: a category-theoretic perspective.

Now, quantum entanglement is a sneaky way for two distant particles to be correlated. A wormhole is a sneaky way for two distant particles to be connected. Could this be hinting at yet another analogy between quantum mechanics and our theory of spacetime? Perhaps one that deserves a category-theoretic treatment?

Last summer, when Jamie Vicary and I were both at the Centre for Quantum Technologies, we figured out something interesting about this. We wrote a paper about it, which is done now:

John Baez and Jamie Vicary, Wormholes and entanglement.

I’d like to explain a bit of it here, because it uses 2-categories in a cute way.

$MathML-enabled post (click for more details).$

Disclaimers

First, I want to emphasize that Jamie and I are not making any claims about the firewall problem. In particular, we’re not claiming that EPR = ER is a way to solve the firewall problem.

Second, we’re not claiming that in our universe, every quantum-entangled pair of particles is connected by a wormhole.

Third, I’m not going to explain the firewall problem here. I don’t feel I have a deep understanding of it — and in fact, I wouldn’t be shocked if it gently dissolves when people think about it carefully enough. So, if you want to get a feel for this problem, but don’t feel quite up to the technical literature, I recommend starting with these blog articles:

George Musser, When you fall into a black hole, how long have you got?
John Preskill, Is Alice burning? The black hole firewall controversy.
Joe Polchinski, Black Holes, complementarity, and firewalls.

I’ve listed them in roughly increasing order of how much physics you need to know to enjoy them, but they’re all good in different ways. The quantum information theorist John Preskill also wrote a nice intro to Maldacena and Susskind’s work:

John Preskill, Entanglement = wormholes.

Wormholes and pair creation

Okay, so let me tell you what I’m actually going to tell you about. Jamie and I did some calculations that work in a simplified setup where spacetime is just 3-dimensional, and nothing about spacetime matters except its topology. This is called a 3-dimensional topological quantum field theory, or 3d TQFT for short.

3d TQFTs are good for describing quantum gravity in a fictitious world where spacetime is 3-dimensional and time is no different from space. At a more practical level, they’re also good for describing thin films of certain special substances at very low temperatures! Some people want to use these films to make topological quantum computers.

Here’s the interesting thing: in this setup, the creation of a particle-antiparticle pair can be reinterpreted as the formation of a wormhole. The particle and its antiparticle are the opposite ends of the wormhole! See, we can interpret this picture two ways:

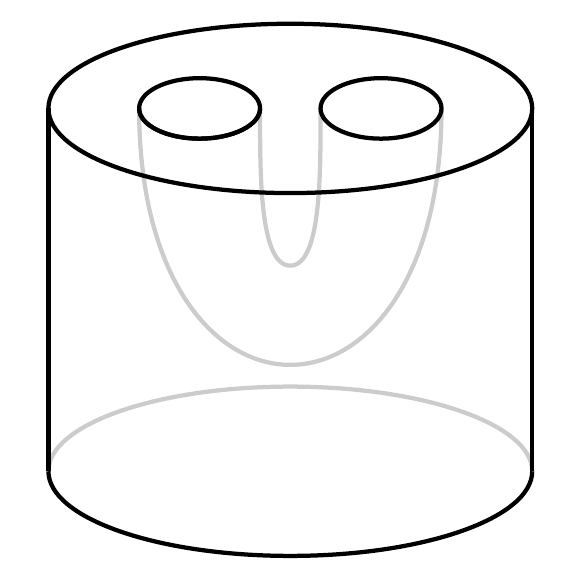
In one way of interpreting this picture, we’re looking at a chunk of spacetime with a curved tube removed. Reading it from bottom to top, space starts out as a disk and ends up as a disk with two holes. So, a particle-antiparticle pair is being created!

In the other way of interpreting this picture, we think of that curved thing as a wormhole: a handle connecting two distant part of space. Reading from bottom to top, space starts out as a disk and ends up as a disk with a handle attached. So, a wormhole is being formed!

If this seems confusing, don’t worry: I’ll explain it more precisely later.

The idea that particle-antiparticle pairs could be wormhole ends is an old one, going back to the paper by Einstein and Rosen. It’s especially cute for electrically charged particles. When it seems the electric field is diverging, coming out of a particle, maybe it’s really just flowing through a wormhole and coming out one end… and flowing in the other end, which would thus look like a particle of the opposite charge.

The idea has been kicking around for a long time. John Wheeler was especially fond of it: he called it ‘charge without charge’. But the discovery of 3d TQFTs gave us a context where we can make this idea precise and calculate with it.

This lets us relate quantum entanglement of particle-antiparticle pairs to wormholes. Indeed, we can compute what happens when a wormhole forms in a 3d TQFT, and use that to compute the state of the resulting particle-antiparticle pair.

The particle and antiparticle act entangled! They even act like they’re ‘completely’ entangled: every piece of information about the particle at one end of the wormhole is encoded in information about its antiparticle at the other end.

This entanglement is, however, a kind of sham. The particle and its antiparticle act entangled, but they have no choice about this, since they are not really separate things. They are just two views of the same thing: the wormhole. True entanglement arises when two independent things are correlated in a certain way. It doesn’t really count as entanglement when something is correlated with itself.

The fact that the entanglement is ‘fake’ was crucial for Maldacena and Susskind, who used it to get around a key aspect of the firewall problem: the so-called ‘monogamy of entanglement’. Just as it’s against the rules to be married to two people, a quantum system can’t be entangled with two others. But ‘fake’ entanglement isn’t monogamous.

Jamie Vicary and I make the concept of fake entanglement precise in our paper, but I don’t feel like talking about that now. Instead, I want to say more about how the creation of a particle-antiparticle pair can be reinterpreted as the formation of a wormhole. This is where 2-categories come in…

Wormholes and pair creation: the 2-categorical view

In our simplified setup where spacetime is just 3-dimensional, space is just 2-dimensional, and the formation of a wormhole looks like this:

This process goes from a disk to a disk with a handle attached. But the disk itself can be seen as a process going from the empty set to a circle… and so does the disk with a handle attached. A ‘process between processes’ is a 2-morphism in a 2-category. So, the formation of a wormhole is actually a 2-morphism, like this:

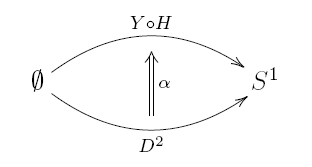
Here $\emptyset$ is the empty set, $S^1$ is the circle, and $D^2$ is the disk. $Y \circ H$ is the disk with a handle attached… but why am I calling it that?

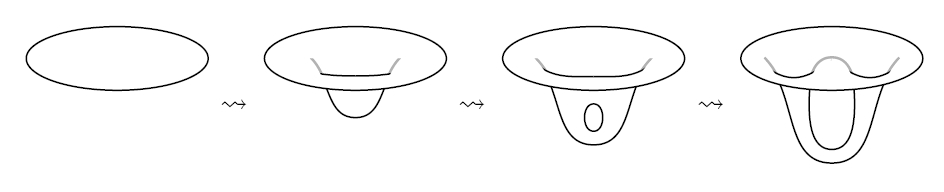
Here’s why. The disk with a handle attached can be chopped into two pieces: a handle, and a disk with two holes:

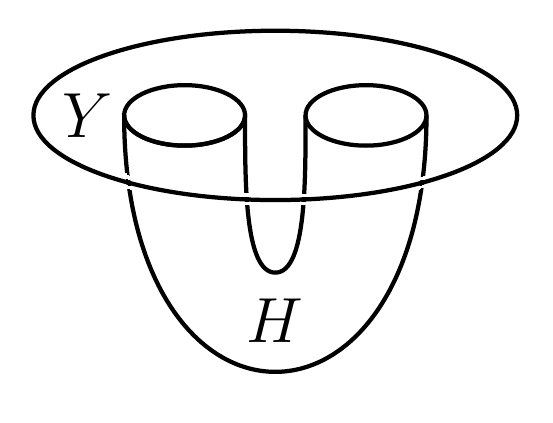
The handle goes from the empty set to the disjoint union of two circles:

$H : \emptyset \to S^1 \sqcup S^1$

The disk with two holes goes like this:

$Y : S^1 \sqcup S^1 \to S^1$

So, the disk with a handle is the composite

$Y \circ H : \emptyset \to S^1$

Okay, so we’ve sliced and diced the process of wormhole formation and seen how it’s a 2-morphism in a 2-category. What about the process of creating a particle-antiparticle pair? What does that look like?

It looks like this:

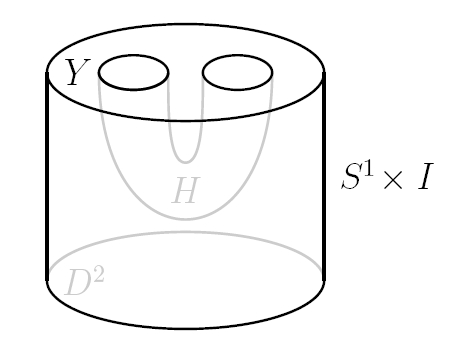
We read this from bottom to top. Space starts out as a disk. As time passes, a particle-antiparticle pair forms. When they’ve formed, space is a disk with two holes. (You see, in 3d TQFTs a particle can be treated as a hole cut out of space, or ‘puncture’.)

Here’s a 2-categorical diagram for this process of pair creation:

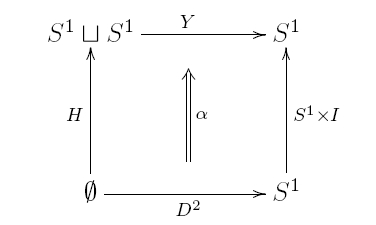
At the start, space is a disk — and as before, we think of this disk as going from the empty set to the circle:

$D^2 : \emptyset \to S^1$

As time passes, space turns into a disk with two holes, namely

$Y: S^1 \sqcup S^1 \to S^1$

As this happens, the circle doesn’t change, but the empty set turns into two circles, thanks to the handle

$H : \emptyset \to S^1 \sqcup S^1$

Now here’s the punchline. Take the square diagram:

Compose the left and top arrows, and compose the bottom and right ones. The bottom and right ones compose to give a disk:

$(S^1 \times I) \circ D^2 = D^2$

so we get a diagram we’ve already seen:

This is the diagram for wormhole formation! So, pair creation is just wormhole formation in disguise.

2-categorical remarks

Finally, here are some remarks that may be too categorical, and even too 2-categorical, for most readers to enjoy.

The ‘bigon’ here is how we draw a morphism in a 2-category:

But the square here is how we draw a morphism in a double category:

There’s a standard trick for getting double categories from 2-categories, due to Ehresmann, and that’s what we’re using here. It’s fairly common for people to study TQFTs using 2-categories. Indeed, Jamie is writing a huge multi-part paper on this with Bruce Bartlett, Chris Douglas and Chris Schommer-Pries, which will be really exciting when it comes out, assuming hell hasn’t frozen over yet. It’s less common for people to study TQFTs using double categories, but Jeffrey Morton has:

Jeffrey Morton, Extended TQFTs and quantum gravity.
Jeffrey Morton, Double bicategories and double cospans.

The advantage of double categories is that they let us study cobordisms-between-cobordisms where the boundary of space changes with time… as in pair creation. Since Jeffrey was my grad student, I was primed to think about this issue.

Here’s another thing, which Jamie and I were reluctant to include in our paper. You can get a 3d TQFT $Z$ from a modular tensor category $\mathbf{C}$ , and then

$Z(S^1) = \mathbf{C}$

Since a hole in space acts like a particle, and cutting out a hole in space leaves a circle as boundary, $\mathbf{C}$ plays the role of the ‘2-Hilbert space of particle types’. $\mathbf{C}$ has a basis of simple objects which are the various types of particles.

The 2-Hilbert space for a pair of particles is then

$Z (S^1 \sqcup S^1) = \mathbf{C} \boxtimes \mathbf{C}$

where $\boxtimes$ is the tensor product of 2-Hilbert spaces. So when we apply our TQFT to a handle

$H : \emptyset \to S^1 \sqcup S^1$

we get

$Z(H) : \mathrm{Hilb} \to \mathbf{C} \boxtimes \mathbf{C}$

and this functor is determined by its value on $\mathbb{C} \in \mathrm{Hilb}$ , which is

$\bigoplus_\sigma \sigma \boxtimes \sigma^* \in \mathbf{C} \boxtimes \mathbf{C}$

where $\sigma$ ranges over the simple objects of $\mathbf{C}$ , and $\sigma^*$ is the dual of $\sigma$ .

Translating back into physics: the two ends of the wormholes act like particles. These particles can be of any type whatsoever, but if one end happens to be a particle of type $\sigma$ , the other end has to be the corresponding antiparticle, $\sigma^*$ . So, you could call $\bigoplus_\sigma \sigma \boxtimes \sigma^*$ the space of states of a particle-antiparticle pair.

And, this space of states is a categorified version of a completely entangled state! In ordinary quantum mechanics, we could have a Hilbert space $\mathcal{H}$ with a basis $e_i$ , and a completely entangled state would be something like

$\sum_i e_i \otimes e_i \in \mathcal{H} \otimes \mathcal{H}$

(up to normalization). Now we’ve got a 2-Hilbert space $\mathbf{C}$ and

$\bigoplus_\sigma \sigma \boxtimes \sigma^* \in \mathbf{C} \boxtimes \mathbf{C}$

It’s the same idea, one level up! We could call this ‘2-entanglement’.

Even better, we have a kind of microcosm principle thing going on. In higher category theory, little things often naturally live in bigger things that are categorified versions of themselves. For example, monoids naturally live in monoidal categories. There are many other examples, too. This is called the ‘microcosm principle’.

In the situation here, we’ve already seen the space of states of the particle-antiparticle pair is 2-entangled. But the formation of a wormhole creates an element of this space of states: a particle-antiparticle pair in a particular state. And this state is itself entangled!

Jamie explain this in more detail in our paper, starting at equation (4). But we didn’t mention that the entanglement of the state of the particle-antiparticle pair is ‘riding’ the 2-entanglement of the space of states of this pair. You have to really like higher categories to care about an observation like this.

Posted at January 19, 2014 10:37 AM UTC

TrackBack URL for this Entry: https://golem.ph.utexas.edu/cgi-bin/MT-3.0/dxy-tb.fcgi/2684

43 Comments & 0 Trackbacks

Re: Wormholes and Entanglement

That’s a very cute paper! I wish I understood TQFTs better in order to really make sense of what’s going on. So here are some basic questions.

First, you write: “In the presence of topology change, the time evolution operators in a TQFT are not unitary, only linear”. I’ve noticed this before and it confused me. How am I supposed to think of this in terms of physics?

Second, the way in which the double category approach handles (no pun intended ;-)) space is such that space itself is a morphism in a category, having an ingoing and an outgoing boundary. Again, what does this mean physically? I can see that space may have a boundary, but why does it come in two parts?

I can see that both questions have to do with the fact that objects in cobordism categories have duals, but the physical meaning eludes me…

Posted by: Tobias Fritz on January 19, 2014 6:45 PM | Permalink | Reply to this

Re: Wormholes and Entanglement

$MathML-enabled post (click for more details).$

Tobias wrote:

I’ve noticed this before and it confused me. How am I supposed to think of this in terms of physics?

I think about it in terms of the analogy between space and state, spacetime and process. Spacetime is a cobordism between two manifolds representing space

$M : S \to S'$

If we reverse the arrow of time, we can think of it going the other way, giving

$M^\dagger : S' \to S$

In the cases we’re most familiar with in everyday life $M^\dagger$ is the inverse of $M$ . So, if apply some quantum field theory $Z$ , we see that $Z(M^\dagger)$ is the inverse of $Z(M)$ . In other words, $Z(M)$ is unitary.

But if $M^\dagger$ fails to be the inverse of $M$ , it would be weird to expect $Z(M^\dagger)$ to be the inverse of $Z(M)$ . This is typical when $M$ involves ‘topology change’, like this:

Second, the way in which the double category approach handles (no pun intended ) space is such that space itself is a morphism in a category, having an ingoing and an outgoing boundary.

Actually this is also true in the more common 2-category approach, which is a bit simpler, so I’ll talk about that. (The idea is the same.)

Again, what does this mean physically? I can see that space may have a boundary, but why does it come in two parts?

It’s just convenient to formalize things this way when we want to stick chunks of space together to form bigger chunks. The category in which ‘spaces’ are morphisms is a compact dagger-category. So, if we have a chunk of space

$S : \Sigma_1 \to \Sigma_2$

going from some boundary $\Sigma$ to some boundary $\Sigma'$ , we’re free to rewrite it as

$S' : \Sigma_1 \sqcup \Sigma_2 \to \emptyset$

using the compactness, or

$S^\dagger : \Sigma_2 \to \Sigma_1$

using the dagger-structure, or

$S^\dagger' : \Sigma_2 \sqcup \Sigma_1 \to \emptyset$

and so on. It doesn’t matter how we divide the boundary of space into a source and target — except when we want to compose two chunks of space, where by convention we take some components of the boundary of a manifold and call their union the ‘source’, and the rest the ‘target’, and attach the target of one chunk of space to the source of the next.

In short, we have all the flexibility we want. People have made up other formalisms that seem (to them) more natural, but they’re equivalent, and most people have decided it’s best to use category theory even for situations where dividing the ‘boundary’ of a morphism into two pieces — the source and target — is a bit artificial.

Posted by: John Baez on January 19, 2014 9:09 PM | Permalink | Reply to this

Re: Wormholes and Entanglement

$MathML-enabled post (click for more details).$

From the diagram, it looks to me that if you interpret it as representing particle-antiparticle creation, then it has two dimensions of space, and one dimension of time, where you go from the past to the future as you look from the bottom to the top of the diagram. If you were representing particle-antiparticle creation assuming point particles, the worldlines of the particles would form a parabola. If you assume that the particles were closed strings in string theory, their worldsheets would form a tube similar to the diagram. On the other hand, if you interpret the diagram as representing a wormhole, then it has three dimensions of space, and zero dimensions of time, and represents a static picture of a wormhole that is not evolving in time. Therefore, particle-antiparticle creation would be dual to the existence of a wormhole, but not the formation of a wormhole, which is a dynamic process, and which would require an additional dimension to represent, and that you represented elsewhere in the article by what could be described as a few selected frames of a movie. The entire movie, representing the formation of a wormhole, would not be dual to particle-antiparticle creation, which would be represented by the most right hand image in sequence, but would instead represent a spectrum of possible particle interactions, only one of which would be particle-antiparticle creation.

Also, if you imagine that all particles are the ends of wormholes, then there would be equal numbers of particles and antiparticles. In the real world, obviously, there are far more particles than antiparticles.

Posted by: Jeffery Winkler on January 24, 2014 10:39 PM | Permalink | Reply to this

Re: Wormholes and Entanglement

$MathML-enabled post (click for more details).$

Hi Tobias. I have thought a lot about the question of the physical interpretation of $Z(M)$ , where $M$ is some topology-changing spacetime process. In this case, as you say, $Z(M)$ is not necessarily unitary – so we have a problem, because only unitary operators have a straightforward interpretation as describing dynamical processes in quantum theory.

Here’s my perspective in a very general sense. Suppose some events are taking place, about which you and I would like to gather data. You arrange some sensors $S$ to collect this data, and I arrange my own set $S'$ . These two sets have some fixed relationship, depending on the different ways we choose to arrange them, and you could think of this as a method $M: S \to S'$ to rearrange your sensors into my sensors. (Basic steps might be ‘add a sensor here’, ‘remove this sensor’, or ‘move this sensor from here to there’.) This method could be reversed, giving a new method $M ^\dagger: S' \to S$ .

Now suppose the events take place, our sensors do their jobs, and we each receive our respective data sets. Your data set is $Z(S)$ , and you want to know what data I received. Then your best guess given by some map $Z(M)$ , which is a map transforming your statistics into my statistics. If we arranged our sensors in essentially equivalent ways, such that my data can be reconstructed exactly from your data and vice versa, then $Z(M)$ will be an invertible map, with inverse $Z(M^\dagger)$ . But in general, of course, this will not be the case — and then it’s totally non-mysterious that if we start with your data set, use that to work out a best guess for my data set, and then use that to work out a best guess of your original data set, we’re going to get something different to what we started with. (Anyone who has played with online language translation tools will recognize this phenomenon!)

This set of ideas can be used to interpret topology-changing processes in a topological quantum field theory, in a mathematically-precise way. The set of events is some particle physics experiment; $S$ is some surface surrounding the experiment on which you place your detectors; and $S'$ is some other surface surrounding the experiment on which I place my detectors. If these surfaces are both spheres, with the same topology, then $Z(M)$ will be a unitary linear map, because we will both be able to infer just the same information about the quantum state of the underlying events we’re measuring.

But if our surfaces are topologically inequivalent – for example, your detectors $S$ are arranged in a torus, and mine $S'$ are arranged in a sphere that surrounds your torus – you will be able to collect a lot more data than me. There is nevertheless a perfectly good manifold $M:S \to S'$ that describes how your surface sits inside my surface, and we can use the nonunitary linear map $Z(M)$ to turn your data into a best-possible approximation of my data. We can also use $Z(M ^\dagger)$ to turn my data into a best-possible approximation of your data. But since we carried out such different experiments, it is not at all mysterious that $Z(M^\dagger) \circ Z(M)$ will not be the identity.

This way of interpreting topological quantum field theory comes originally from Louis Crane, and his ‘skin of observation’ idea.

Posted by: Jamie Vicary on January 20, 2014 12:01 AM | Permalink | Reply to this

Re: Wormholes and Entanglement

$MathML-enabled post (click for more details).$

That is very cool. I have never heard of any kind of interpretation like this in terms of sensors and their arrangement, and I would like to learn a little more about its current status. A quick google got me Crane’s (original?) paper. Is that still going to be the place to start, or could you suggest any other references? Thanks!

Posted by: Dan Carney on January 20, 2014 7:13 PM | Permalink | Reply to this

Re: Wormholes and Entanglement

$MathML-enabled post (click for more details).$

Louis Crane talks about ‘skins of observation’ in a couple of papers that I know of, including the one that you linked to. Both of them are about 2 decades old.

I made up the stuff about sensors :).

Posted by: Jamie Vicary on January 20, 2014 8:28 PM | Permalink | Reply to this

Re: Wormholes and Entanglement

$MathML-enabled post (click for more details).$

In re: unitarity If we take the cobordism for disk to disk with handle and flip it (up or down) we get a cobordism from surface to itself but not a cylinder. Is that the point? So better than just linear but not unitary aka _?/

Posted by: jim stasheff on January 22, 2014 8:52 PM | Permalink | Reply to this

Re: Wormholes and Entanglement

$MathML-enabled post (click for more details).$

Great question, Tobias; great answers, Jamie (and John, earlier). I have been wondering the same thing, on and off, about unitarity vs. linearity. John’s point that that $M^\dagger M$ is not the identity in the cobordism category is quite clear, so one wouldn’t expect unitarity after applying the functor Z, and Jamie you help clear up the significance of that fact.

About the sensors on a torus gathering more data than those on a sphere surrounding the torus, is it possible to make that more concrete? One thinks of something like an electromagnetic example, with the torus enclosing a loop of wire with an electric current circulating in it, and the sensors on the torus being able to measure the curl of an induced electric field, but I’d want to think a bit more about whether (or not!) the sensors on the sphere could recover the same data. (In flat-space electromagnetism, I guess maybe they could? Not sure offhand.) Of course that idea isn’t formulated in TQFT terms… but I’d like to get a more concrete understanding of your idea. Or, could you give an example where one is comparing sensors on a disc, to ones on a disc with two circles cut out of it? That would be nice since it would involve the the M that John used in his example of $M^\dagger$ not being $M^{-1}$ , i.e. the one in your paper, pair-creation/wormhole formation.

Also, I’m curious about probability-conservation in the nonunitary case. If we were dealing with a functor Z from a cobordism category to Hilb, then I would worry that a linear but nonunitary map could fail to preserve probability. I would then feel uncomfortable about a physical interpretation. One might hope to obtain a reasonable interpretation by viewing the linear map as a Kraus operator. But then one would want a set of maps. Perhaps these would come from a set of functors Z? Or more likely, a single functor to some category other than Hilb, such as lists of Hilbert spaces, giving with Z giving us a linear operator on each one, in such a way that viewing these as Kraus operators gives us an explicitly Kraus-decomposed quantum operation (trace-preserving CP map). Or maybe (as I think John suggests somewhere in this discussion) we should just go to a category of CP maps straightaway. Another question I have for you about this, since I don’t understand 2-Hilbert spaces very well yet, is whether dealing with 2-Hilbert spaces as the target of Z help with this? Can Z from a 2-category of cobordisms to 2-Hilb already represent CP maps?

Posted by: Howard Barnum on October 17, 2014 6:59 PM | Permalink | Reply to this

Re: Wormholes and Entanglement

$MathML-enabled post (click for more details).$

Just correcting the spelling of the link associated with my name (i.e., to my website).

Posted by: Howard Barnum on October 23, 2014 9:31 PM | Permalink | Reply to this

Re: Wormholes and Entanglement

$MathML-enabled post (click for more details).$

You’re asking great questions about making my ‘sensors’ idea more precise. I haven’t really thought it through to the level of mathematical details, unfortunately, so I can’t really give any more details. There is nothing particularly quantum about the idea, so it could be a way of interpreting a ‘classical’ TQFT valued in stochastic processes, for example. John mentions somewhere else on this page the idea of investigating TQFTs valued in C*-algebras and completely-positive maps; I think that’s a great idea.

If $Z(M)$ is a non-isometric linear map between Hilbert spaces, then it definitely doesn’t preserve probability, and it doesn’t have a straightforward interpretation as physical process. So one thing to do is change our category. In this completely positive map category, every morphism has a good interpretation.

The extension to 2Hilb corresponds to defining your invariants on cobordisms of codimension 2. I don’t think this is necessary to investigate this phenomenon. For example, the symmetric monoidal category of compact 1-dimensional manifolds and diffeomorphism classes of 2d cobordisms already has plenty of topology-changing maps.

Posted by: Jamie Vicary on October 24, 2014 4:55 PM | Permalink | Reply to this

Re: Wormholes and Entanglement

$MathML-enabled post (click for more details).$

Thanks, both, for these lucid explanations! I’ll have to think about Jamie’s answer a bit more, so for now this is a reply to John.

John wrote:

But if $M^\dagger$ fails to be the inverse of $M$ , it would be weird to expect $Z(M^\dagger)$ to be the inverse of $Z(M)$ .

Well, what if our target category happens to be a groupoid in which the dagger happens to be given by taking the inverse? But I agree that it would be weird in the case of $n\mathbf{Hilb}$ , though.

Now I realize that my question should have been more like, “What happens to the Born rule?” I think this is what Jamie answered :-)

About the question of why the boundary of space comes in two parts, John explained:

It’s just convenient to formalize things this way when we want to stick chunks of space together to form bigger chunks. [..] It doesn’t matter how we divide the boundary of space into a source and target — except when we want to compose two chunks of space, where by convention we take some components of the boundary of a manifold and call their union the ‘source’, and the rest the ‘target’, and attach the target of one chunk of space to the source of the next.

Right. That makes perfect sense, but I’m not convinced that one has to split the boundary in that way in order to make sense of sticking chunks of space together. Say we have chunks of space $S_1$ and $S_2$ and injections $\Sigma\hookrightarrow S_1$ and $\bar{\Sigma}\hookrightarrow S_2$ , where we need to make sure that these maps are orientation-preserving in the appropriate sense. Then this data is enough to stick $S_1$ and $S_2$ together along $\Sigma$ without having decomposed all the rest of the boundary of either into an ‘ingoing’ and an ‘outgoing’ part!

Posted by: Tobias Fritz on January 20, 2014 9:33 AM | Permalink | Reply to this

Re: Wormholes and Entanglement

$MathML-enabled post (click for more details).$

Tobias wrote:

Now I realize that my question should have been more like, “What happens to the Born rule?” I think this is what Jamie answered :-)

Jamie’s answer was better than mine: more ‘operational’ and more ‘physical’. Mine was more a way of saying that it would be very unnatural to expect time evolution to be unitary in the presence of topology change if we expect a beautiful tight connection between spacetime topology and quantum mechanics (as we have in TQFTs).

To dig deeper into the physics of topology change, I think it might be interesting to study things like TQFTs where the target of the functor $Z$ is something like the category of C*-algebras and completely positive maps.

That makes perfect sense, but I’m not convinced that one has to split the boundary in that way in order to make sense of sticking chunks of space together.

No, we definitely don’t have to. The existing formalism is just a convenient way to talk about gluing chunks of space together while working within the framework of category theory. It’s good for people who like categories. We could also use other frameworks, like operads.

Posted by: John Baez on January 20, 2014 11:18 AM | Permalink | Reply to this

Re: Wormholes and Entanglement

$MathML-enabled post (click for more details).$

To dig deeper into the physics of topology change, I think it might be interesting to study things like TQFTs where the target of the functor $Z$ is something like the category of C*-algebras and completely positive maps.

With Jamie’s answer in mind, that sounds like a great idea! There is some stuff about (one possible definition of) 2-C*-categories that may be relevant here…

Posted by: Tobias Fritz on January 20, 2014 7:04 PM | Permalink | Reply to this

Re: Wormholes and Entanglement

$MathML-enabled post (click for more details).$

Hi Tobias. The question of why we should split the boundary of a cobordism into ‘incoming’ and ‘outgoing’ parts is an extremely interesting one. It is one of the key distinctions between the functorial approach to TQFT begun by Atiyah, and work in a non-categorical style such as these famous notes by Walker. This is very much a modern issue, in the sense that both styles have their proponents, and there is no settled consensus as to which is the ‘better’ approach.

I favour the categorical style, in which the division between incoming and outgoing boundaries is hard-coded. For me, a key advantage is that this gives the subject an algebraic flavour, in the following sense. Consider a monoidal category $\mathbf{C}$ , with tensor product defined by a functor ${}\otimes{}: \mathbf{C} \times \mathbf{C} \to \mathbf{C}$ . We could say that the tensor product operation $\otimes$ has three ‘boundary components’, given by three copies of $\mathbf{C}$ , and that these are separated into two ‘incoming components’ and one ‘outgoing component’. Is this essential? Probably not – I’m sure you could develop a theory of monoidal categories in which this separation is not hard-coded. But it probably wouldn’t be very nice; there are extremely good reasons reasons that algebra is developed as a theory of binary operations.

The reason this is so nice to have is that TQFTs can be classified in terms of algebraic structures — for example, 2d TQFTs are classified by commutative Frobenius algebras, and 3d TQFTs extended to 1-manifolds are classified by modular tensor categories. This is all made a lot easier if our cobordisms are given in ‘algebraic style’ from the beginning, with fixed ‘incoming’ and ‘outgoing’ components.

More philosophically, this is also how we experience chunks of time in our everyday experience, as having clearly separated past and future boundaries. I can’t help feeling this is deeply related, although I couldn’t say anything mathematically nontrivial about it.

Posted by: Jamie Vicary on January 20, 2014 11:08 AM | Permalink | Reply to this

Re: Wormholes and Entanglement

$MathML-enabled post (click for more details).$

Fascinating thoughts, Jamie!

I’m sure you could develop a theory of monoidal categories in which this separation is not hard-coded.

Something like this has been done in Higher Operads, Higher Categories, where a definition of “unbiased monoidal category” is given in which there is a tensor product functor for any finite arity. But as you say, there is a sense in which it’s enough to consider binary tensor products; I think this is Tom’s Theorem 3.2.4.

Funnily enough, I just attended a talk of Pierre-Louis Curien in which he mentioned so-called structads, which are new operad-like gadgets defined roughly as follows. One does not distinguish between the inputs and outputs of an operation, but every operation simply has an arity given as a set of wires with labels. The set of admissible labels is equipped with an involution. Now two wires belonging to two operations can be wired together whenever their labels are involutes of each other. According to Pierre-Louis, this is work of François Lamarche, but no preprint is available yet. It reminded me immediately of this discussion here!

Posted by: Tobias Fritz on January 20, 2014 7:26 PM | Permalink | Reply to this

Re: Wormholes and Entanglement

$MathML-enabled post (click for more details).$

That sounds interesting, and a bit topological in spirit. Perhaps structads are to operads as pivotal categories are to monoidal categories?

Posted by: Jamie Vicary on January 20, 2014 9:33 PM | Permalink | Reply to this

Re: Wormholes and Entanglement

$MathML-enabled post (click for more details).$

Structads sound quite a bit like cyclic or modular operads. Did Curien have any comment regarding that?

Posted by: Todd Trimble on January 20, 2014 11:05 PM | Permalink | Reply to this

Re: Wormholes and Entanglement

$MathML-enabled post (click for more details).$

Yes, cyclic operads were discussed as well, but modular operads were not. Actually, Lamarche’s paper on structads is available here; see p.27 for a remark saying that cyclic operads are equivalent to those structads in which the set of labels is a singleton (with trivial involution).

I don’t understand any of this well enough to say more about it. My idea is that something like this will be able to accomodate manifolds with boundary without assuming this boundary to come in two parts, but this may be very naive…

Posted by: Tobias Fritz on January 21, 2014 3:31 PM | Permalink | Reply to this

Re: Wormholes and Entanglement

$MathML-enabled post (click for more details).$

Tobias wrote:

My idea is that something like this will be able to accomodate manifolds with boundary without assuming this boundary to come in two parts…

Something like this will work if instead of cyclic operads you use ‘completely permutative operads’. But it’s really not worth it, in my opinion.

Remember: in a ‘permutative operad’, often just called an ‘operad’, an operation has $n$ inputs and one output, and given any permutation of the inputs we can get a new operation in which the inputs are permuted.

In a ‘cyclic operad’, an operation has $n$ things which you can think of as either inputs or outputs, and given any cyclic permutation of these $n$ things we get a new operation.

Similarly, we can make up ‘completely permutative operads’, where an operation has $n$ input/outputs, and given any permutation of these $n$ things we get a new operation.

But James Dolan and I prefer to think of these as ‘compact PROPs’.

Remember, in a ‘PROP’ an operation has $n$ inputs and $m$ outputs, and given any permutation of the inputs, and any permutation of the outputs, you get a new operation.

But a PROP is just another way to think of a strict symmetric monoidal category where all objects are of the form $x^{\otimes n}$ for some fixed object $x$ . The set of operations with $n$ inputs and $m$ outputs is just the set of morphisms $hom(x^{\otimes n}, x^{\otimes m})$ .

If this symmetric monoidal category is compact, we call our PROP a ‘compact PROP’.

In a compact PROP we start by retaining the distinction between inputs and output that so distresses you. However, because we can freely permute inputs and outputs, we can turn inputs into outputs and vice versa, so it becomes a ‘difference that doesn’t make a difference’.

If this still annoys you, you could work with ‘completely permutative operads’ where the distinction between inputs and outputs was never there to begin with. A similar impulse is the reason the topologist Frank Quinn invented ‘domain categories’, where morphisms don’t have a domain and codomain, just a domain.

But I predict these approaches, being equivalent to much more popular approaches and offering little benefit except the feeling of greater righteousness, will never catch on.

More important, I think, is knowing formalisms that handle various different degrees of ability to permute inputs and/or outputs.

So, don’t forget ‘nonpermutative operads’, also known as ‘multicategories’, where our operations have $n$ inputs and one output, and we cannot permute the inputs.

Also, ‘PROs’, where our operations have $n$ inputs and $m$ outputs, and we can neither permute inputs nor outputs.

Posted by: John Baez on January 21, 2014 5:20 PM | Permalink | Reply to this

Re: Wormholes and Entanglement

$MathML-enabled post (click for more details).$

Thanks, John, for this beautiful summary! It fits in nicely with Jamie’s remark about classifying TQFTs in terms of algebraic structures. So I’ll shut up now ;)

Posted by: Tobias Fritz on January 21, 2014 6:19 PM | Permalink | Reply to this

Re: Wormholes and Entanglement

In the presence of topology change, the time evolution operators in a TQFT are not unitary, only linear

If we accept this for a QFT in the real world, too, then the black hole information paradox evaporates.

Posted by: Toby Bartels on February 10, 2014 7:52 AM | Permalink | Reply to this

Re: Wormholes and Entanglement

$MathML-enabled post (click for more details).$

I would like to dig a bit deeper into the idea of ‘2-entanglement’. I think it’s all about units.

For starters, note that the handle

$H : \emptyset \to S^1 \sqcup S^1$

is the counit of an adjunction. If we had a 2d TQFT, say $Z$ , this would give a linear map

$Z(H) : \mathbb{C} \to Z(S^1) \otimes Z(S^1)$

which is again the unit of an adjunction. This linear map is a way of describing the completely entangled state

$Z(H)1 = \sum_i e_i \otimes e_i$

where $e_i$ is any basis of $Z(S^1)$ .

But we’re looking at a 3d TQFT, so everything becomes more elaborate. Applying this 3d TQFT to the handle gives a linear functor

$Z(H) : \mathrm{Hilb} \to Z(S^1) \boxtimes Z(S^1)$

where $Z(S^1) = \mathbf{C}$ is a modular tensor category. This linear functor is a way of describing the ‘completely 2-entangled space of states’

$Z(H) \mathbb{C} = \bigoplus_\sigma \sigma \boxtimes \sigma^*$

The ‘creation of a handle’

is, I believe, also a unit. However, it’s at a higher categorical level: if the handle is a 1-morphism, this is a 2-morphism. Is it a unit of a unit? I don’t have time to figure this out right now, but I really want to know. It may be a slightly disguised unit of a unit.

Applying $Z(H)$ to the creation of a handle, we get a completely entangled state of the particle-antiparticle pair.

So I’m guess there two units going on, at the 1-morphism and 2-morphism levels, and this produces ‘entanglement riding 2-entanglement’.

Posted by: John Baez on January 20, 2014 12:42 PM | Permalink | Reply to this

Re: Wormholes and Entanglement

$MathML-enabled post (click for more details).$

It’s the slightly disguised unit of the adjunction ‘copants $\dashv$ pants’. The ‘disguise’ is that the unit of that adjunction should be on the cylinder, not the disc – so to lift the disguise, put a copants on top of every picture in the little movie you gave in your comment.

If you take the counit of this adjunction ‘copants $\dashv$ pants’, and disguise it in the same way, it takes the form of ‘snipping the wormhole’. So, imagine going ahead and snipping through the bottom part of the wormhole in the 4th image in your sequence, with a pair of metaphysical scissors. You are left with two wounds, which are newly-exposed boundary circles – imagine these ‘heal’ immediately, being patched with two little discs that we add. Mathematically, this is removal of a 2-handle. We now have a disc with two little stumps that reach down, and don’t go anywhere – we could imagine these retracting back up, giving a disc.

Overall, the process ‘grow a wormhole, then snip it in two’ would go from the disc to the disc. And in fact the whole thing would be homeomorphic to the identity – that’s just what the adjunction equations say.

Posted by: Jamie Vicary on January 20, 2014 1:19 PM | Permalink | Reply to this

Re: Wormholes and Entanglement

$MathML-enabled post (click for more details).$

Thanks! I’ll think about this.

By the way, due to some sort of dyslexia every time I said ‘counit’ in my previous comment I meant ‘unit’. I’ve gone ahead and fixed that.

Posted by: John Baez on January 20, 2014 2:51 PM | Permalink | Reply to this

Re: Wormholes and Entanglement

$MathML-enabled post (click for more details).$

This is trivial, but in Figure 1(b) of Baez and Vicary I’m guessing that 7 should be a 1.

Posted by: Greg Egan on January 21, 2014 11:38 AM | Permalink | Reply to this

Re: Wormholes and Entanglement

$MathML-enabled post (click for more details).$

Thanks! What a weird typo. There are also some $\boxtimes$ that should be $\otimes$ or vice versa.

The most up-to-date version of the paper, with these errors fixed, can be gotten here.

Posted by: John Baez on January 21, 2014 12:03 PM | Permalink | Reply to this

Re: Wormholes and Entanglement

$MathML-enabled post (click for more details).$

A few things someone should do, brought out in conversations with Stam Nicolis on Google+.

Consider a 2d cobordism

$\Sigma : \emptyset \to S^1 \sqcup \cdots \sqcup S^1$

We can think of $\Sigma$ as a way of making $n$ particles into the ends of a bunch of wormholes. Different choices of $\Sigma$ give different objects in $\mathbf{C} \boxtimes \cdots \boxtimes \mathbf{C}$ . We can think of such an object as a ‘space of allowed states for $n$ particles’—allowed if they are the ends of wormholes in some particular way given by $\Sigma$ . What are the possibilities?

We could try to do this for low $n$ either for some particular famous 3d TQFT, or in general. So far we’ve just done it when $n = 2$ and when $\Sigma$ is a cylinder: the simplest possible wormhole connecting two particles.

$X : S^1 \sqcup \cdots \sqcup S^1 \to S^1$

be the disk with $n$ punctures. Consider a 3d cobordism

$M : D^2 \Rightarrow X \circ \Sigma$

Think of this as a way for the bunch of wormholes to be created starting from a disk. $M$ gives a natural transformation

$Z(M) : Z(D^2) \Rightarrow Z(X) \circ Z(\Sigma)$

In general $Z(M)$ describes the state of the $n$ particles that results from creating the bunch of wormholes having these particle as ends.

What is $Z(M)$ like, exactly? What kinds of entanglement arise? We again have done this only in the simplest nontrivial case.

Posted by: John Baez on January 21, 2014 1:46 PM | Permalink | Reply to this

Re: Wormholes and Entanglement

$MathML-enabled post (click for more details).$

John, if we think of the wormhole as a thin neighborhood of a 1-complex embedded in $D^2\times I$ , then the answer depends on the isotopy class of the embedding of this 1-complex. For example, if the 1-complex is a knotted arc then the relative weights of the particle pairs $a\otimes a^*$ is essentially the collection of colored Jones polynomials of the knot (evaluated at the appropriate root of unity).

If you want to do the general computation, then it is better to think of the complement $D^2\times I \setminus$ {nbd of 1-complex} as built from the bottom (pre-wormhole) part of $D^2\times I$ by adding (3-dimensional) 1-handles and 2-handles. For example, the simple, unknotted wormhole you consider in the initial post can be constructed by adding a single 1-handle to $D^2\times I$ . There are simple formulas for the effect of adding 1- and 2-handles (and even simpler formulas for 0- and 3-handles). The difficult part is changing basis in $Z(Y^2)$ to put oneself in a position to apply these formulas. For that one uses the $S$ and $F$ matrices of the TQFT.

Posted by: Kevin Walker on January 23, 2014 7:46 AM | Permalink | Reply to this

Re: Wormholes and Entanglement

$MathML-enabled post (click for more details).$

As John says, it would be interesting to study what sorts of entanglement can arise in this way. This is something that would presumably be of interest in the TQC community.

Posted by: Jamie Vicary on January 23, 2014 10:48 AM | Permalink | Reply to this

Re: Wormholes and Entanglement

$MathML-enabled post (click for more details).$

By “sorts of entanglement”, do you mean a list of possible particle combinations at the end of the process? Or do you mean the probability that a particular particle combination will occur? Or something else? If the first, the particles $a_1,\ldots,a_n$ can appear at the end of a wormhole with boundary $\Sigma$ if and only if the Hilbert space $Z(\Sigma; a_1,\ldots,a_n)$ is non-zero.

Posted by: Kevin Walker on January 23, 2014 2:08 PM | Permalink | Reply to this

Re: Wormholes and Entanglement

$MathML-enabled post (click for more details).$

I was thinking about the rich structure of the space of entangled states in ordinary quantum information theory. For example, tripartite states come in two equivalence classes of completely entangled states: ‘GHZ type’ and ‘W type’. The tasks these states allow you to perform are quite different.

So, now that we have some interesting new ways to generate a bunch of $n$ -partite entangled states—given by any cobordism from a disk to an $n$ -punctured disk, in the double category sense—we can ask what equivalence classes of entanglement we can produce. Surely this will depend on the cobordism we choose, and also the MTC.

Posted by: Jamie Vicary on January 23, 2014 2:38 PM | Permalink | Reply to this

Re: Wormholes and Entanglement

$MathML-enabled post (click for more details).$

Thanks for the tips, Kevin! By the way, I’ll be in Oxford visiting Jamie Vicary when you show up.

Jamie wrote:

I was thinking about the rich structure of the space of entangled states in ordinary quantum information theory.

I’d be happy for any interesting information about what class of states we can get from various kinds of ‘wormholes’ and various processes of ‘wormhole formation’. But yes, this would be nice.

For example, tripartite states come in two equivalence classes of completely entangled states: ‘GHZ type’ and ‘W type’.

For anyone who doesn’t know this jargon, see Greenberger–Horne–Zeilinger state and W state. These are unit vectors in $\mathbb{C}^2 \otimes \mathbb{C}^2 \otimes \mathbb{C}^2$ , so we’d think about these if we were dealing with the $SU(2)$ Witten–Reshetikhin–Turaev model and a wormhole with 3 ends each labelled by the spin-1/2 representation.

Posted by: John Baez on January 23, 2014 2:57 PM | Permalink | Reply to this

Re: Wormholes and Entanglement

$MathML-enabled post (click for more details).$

Thanks, Jamie and John, for the explanations. Probably it’s more efficient to wait a month and discuss this in person, but here’s one short remark. Once you have produced one state for, say, quasi-particles $a\otimes a \otimes \cdots \otimes a$ , then you can braid them (i.e. braid the wormholes) to approximate any other state you like. This is because for most TQFTs the associated representation of the braid group is dense in the unitary group. (See, e.g., Freedman-Larson-Wang, http://arxiv.org/abs/quant-ph/0001108 .) But perhaps you wanted to produce the GHZ or W states on the nose, without inordinate amounts of braiding?

Posted by: Kevin Walker on January 23, 2014 4:50 PM | Permalink | Reply to this

Re: Wormholes and Entanglement

It is all very interesting. I read the synthesis, and I must read all the linked articles, but I wish to say that strong analogy with the magnetic monopoles of Dirac (that I read in ancient time on Jackson): the wormholes singularity like a wound solenoid for the monopoles. If there are more of an analogy, then some quantization of charge can be obtained. I am thinking that the Maxwell’s equations can be write in a similar way for the matter-antimatter, the gravitational equation must be the same in the time between two annihilations (wire of matter-antimatter with gravitational-magnetic effect); but if this is true, then the Maxwell’s equation can be Einstein field equation with the mass=charge, Newton’s gravitational constant=Coulomb constant, and vice versa. I am thinking that the two holes in a disk (wormholes) can become a hole connected with an open surface, and if there are many particle connected with an open surface then it can be explained the absence of antimatter: the antimatter like an space expansion (negative curvature).

Posted by: Domenico on January 21, 2014 6:46 PM | Permalink | Reply to this

Re: Wormholes and Entanglement

$MathML-enabled post (click for more details).$

As for quantum gravity, I am stuck at the very beginning. How do you make sense of superposition of state functions with no metric preserving mapping between their domains? Which is surely the case with states involving different mass distributions. Is it a silly question?

Posted by: Berényi Péter on January 23, 2014 11:24 AM | Permalink | Reply to this

Re: Wormholes and Entanglement

$MathML-enabled post (click for more details).$

Posted by: Jeffery Winkler on January 24, 2014 10:43 PM | Permalink | Reply to this

Re: Wormholes and Entanglement

$MathML-enabled post (click for more details).$

Jeffrey wrote:

From the diagram, it looks to me that if you interpret it as representing particle-antiparticle creation, then it has two dimensions of space, and one dimension of time, where you go from the past to the future as you look from the bottom to the top of the diagram.

Yes. As you move a horizontal plane up through this picture, you see a hole appear in space and then split in two:

On the other hand, if you interpret the diagram as representing a wormhole, then it has three dimensions of space, and zero dimensions of time, and represents a static picture of a wormhole that is not evolving in time.

No. In the wormhole interpretation of this diagram there are still two dimensions of space and one of time! We still see history unfold as we move a 2d surface up through this picture:

We just move the surface in a different way! It’s not a horizontal plane at each stage. Instead, we let it change with time, like this:

When we do this, the final surface representing space has a wormhole in it! In other words, this time the final surface is $Y$ together with $H$ , not just $Y$ :

So, we’re taking the same chunk of spacetime and interpreting it as two different processes: the creation of a particle-antiparticle pair, and the formation of a wormhole!

All this is explained in a somewhat more technical way in my blog article. But thanks for letting me see that I could have explained it more clearly!

Posted by: John Baez on January 25, 2014 12:31 PM | Permalink | Reply to this

Re: Wormholes and Entanglement

In other words, you're considering two different foliations of the same spacetime into space and time. In the pair-creation case, you're foliating by horizontal slices; in the wormhole-creation case, the foliation is more complicated, but we can understand it by comparing to your picture showing a few individual sheets.

Posted by: Toby Bartels on February 10, 2014 7:41 AM | Permalink | Reply to this

Re: Wormholes and Entanglement

$MathML-enabled post (click for more details).$

Jeffrey wrote:

Also, if you imagine that all particles are the ends of wormholes, then there would be equal numbers of particles and antiparticles. In the real world, obviously, there are far more particles than antiparticles.

True. A few remarks:

1) The situation changes when we consider wormholes with three or more mouths, but there are still constraints.

(The mouths need to act like particles whose corresponding simple objects $\sigma_i \in \mathbf{C}$ tensor together to contain a copy of the unit object in the modular tensor category $\mathbf{C}$ . If you don’t know what a modular tensor category is, think of $\mathbf{C}$ as being similar to a category of group representations, where simple objects are irreducible representations—though $\mathbb{C}$ can’t really be of that form.)

2) Our work applies to 3d TQFTs, so it’s relevant to purely theoretical 3d quantum gravity theories and also to real-world physics of thin films that exhibit topological order, for example those that display the fractional quantum Hall effect. We’re not claiming it applies to real-world particle physics.

3) Nobody is completely sure that some other galaxies aren’t made of antimatter, though there’s little reason to suspect they are and few physicists believe it. One goal of NASA’s Alpha Magnetic Spectrometer is to look for evidence of antimatter galaxies.

4) The usual belief among physicists is that the Universe started with equal amounts of matter and antimatter and this symmetry was later broken through a process of baryogenesis. In 1967 Andrei Sakharov enunciated three necessary conditions for this to be possible: a) violation of the conservation of baryon number, b) violation of C and CP symmetry, and c) conditions far from thermal equilibrium. The latter two are no problem, so it’s just the first that’s a big challenge. We haven’t see violations of baryon number conservation (e.g. proton decay), despite some intensive searches lasting for decades, but it’s predicted in most grand unified theories—and even in the Standard Model under sufficiently extreme conditions.

Posted by: John Baez on January 25, 2014 5:55 PM | Permalink | Reply to this

Re: Wormholes and Entanglement

$MathML-enabled post (click for more details).$

I was trying to catch up a bit on TQFTs, and in Bruce Bartlett’s “Categorical Aspects of Topological Quantum Field Theories” (arXiv:math/0512103) I read something which I find intriguing and don’t understand.

In a three-dimensional TQFT, a Hilbert space $Z(\Sigma_g)$ assigned to a genus- $g$ surface $\Sigma_g$ has a finite dimension which depends on $g$ and on which TQFT is under consideration. More specifically, the value of $dim\, Z(\Sigma_g)$ is given by the Verlinde formula, Eq. (5.35) in the aforelinked. Why should this value be finite? Or, to rephrase the question, what should override my knee-jerk association of “QFT” and “infinite-dimensional Hilbert spaces” when the theory is topological?

Posted by: Blake Stacey on January 28, 2014 1:21 AM | Permalink | Reply to this

Re: Wormholes and Entanglement

$MathML-enabled post (click for more details).$

Blake wrote:

Or, to rephrase the question, what should override my knee-jerk association of “QFT” and “infinite-dimensional Hilbert spaces” when the theory is topological?

Physically speaking, a topological quantum field theory has no local degrees of freedom. What’s going on in any contractible patch of spacetime always looks the same. The only interesting observables are global ones. So, the usual idea that quantum field theories have infinitely many degrees of freedom because the field can wiggle around a lot is gone.

This is part of the story but only part. There are quantum field theories that arise from quantizing a classical field that’s a flat connections for some Lie group $G$ . These have no local degrees of freedom: the interesting observables would include holonomies around noncontractible loops, so, roughly, some Lie group elements. Quantizing, you might expect a Hilbert space as big as $L^2(G)$ — so, infinite-dimensional.

There are quantum field theories like this, but they’re not officially TQFTs. To get a TQFT you could use one of these with a finite group $G$ , to make the Hilbert space finite-dimensional. This is called a Dijkgraaf–Witten model. Or, you could cleverly cook up a gauge theory where the phase space is compact, so you get a finite-dimensional Hilbert space when you quantize it. This is called Chern–Simons theory.

Why the insistence on finite-dimensional Hilbert spaces?

Mathematically, the definition of a TQFT forces the Hilbert spaces to be finite-dimensional, because the partition function of the spacetime $S^1 \times \Sigma_g$ is the trace of the identity operator on the Hilbert space for the surface $\Sigma_g$ — the thing you’re calling $Z(\Sigma_g)$ . Since the partition function is assumed finite, the dimension of this Hilbert space has to be finite! We take the trace of the identity operator because the Hamiltonian is 0 on physical states, as you’d expect in a theory with no local degrees of freedom. It’s like the German village I’m living in now: nothing is happening, locally.

Posted by: John Baez on January 28, 2014 7:55 AM | Permalink | Reply to this

Re: Wormholes and Entanglement

$MathML-enabled post (click for more details).$

Thanks! That clarifies things.

Posted by: Blake Stacey on January 28, 2014 7:03 PM | Permalink | Reply to this

Re: Wormholes and Entanglement

$MathML-enabled post (click for more details).$

Thought experiment, a wormhole and an ideal centrifuge. Wormhole entrance on interior wall of centrifuge, exit in space. Entanglement involves two wormholes interior of first becomes exterior of second and vis versa. This creates gravity.

Posted by: anonymous on February 12, 2014 6:05 PM | Permalink | Reply to this

The n-Category Café

Skip to the Main Content

January 19, 2014