The Scottish Category Theory Seminar
Posted by Tom Leinster
We’re pleased to announce the third meeting of the Scottish Category Theory Seminar, from 2.00 to 5.30 on Thursday 2 December, at the University of Strathclyde (in Glasgow city centre). All are welcome to attend. We have three invited speakers:
- Marcelo Fiore (Cambridge): On higher order algebra
- Peter Johnstone (Cambridge): Hochas and minimal toposes
- Bas Spitters (Nijmegen): Bohrification: topos theory and quantum theory
Abstracts are below. The speakers are chosen to represent category theory in, respectively, computer science, pure mathematics, and physics.
The meeting is generously supported by the Edinburgh Mathematical Society.
Information is on the Scottish Category Theory Seminar home page. Abstracts are there and, for your convenience, below.
If you’re planning to come, it would help us if you sent a quick email saying so. Our email address is scotcats#cis,strath,ac,uk (making the obvious substitutions). This reaches the organizers: Neil Ghani, Alex Simpson, and me.
Here are the abstracts.
Marcelo Fiore: On higher order algebra
The purpose of this talk is to give an overview of recent work on a mathematical theory of higher-order algebraic structure.
Specifically, I will introduce a conservative extension of universal algebra and equational logic from first to second order that provides a model theory and formal deductive system for languages with variable binding and parameterised metavariables. Mathematical theories encompassed by the framework include the (untyped and typed) lambda calculus, predicate logic, integration, etc.
Subsequently, I will consider the subject from the viewpoint of categorical algebra, introducing second-order algebraic theories and functorial models, and establishing correspondences between theories and presentations and between models and algebras. The concept of theory morphism leads to a mathematical definition of syntactic translation that formalises notions such as encodings and transforms in the context of languages with variable binding.
References
M.Fiore, Second-order and dependently-sorted abstract syntax. In Proceedings of the 23rd Logic in Computer Science Conference (LICS’08), pages 57-68, 2008.
M.Fiore and C.-K.Hur. Second-order equational logic. In Proceedings of the 19th EACSL Annual Conference on Computer Science Logic (CSL 2010), LNCS 6247, pp. 320-335, 2010.
M.Fiore and O.Mahmoud. Second-order algebraic theories. In Proceedings of the 35th International Symposium on Mathematical Foundations of Computer Science (MFCS 2010), LNCS 6281, pp. 368-380, 2010.
Peter Johnstone: Hochas and minimal toposes
Recently D. Pataraia introduced the notion of hocha (higher-order cylindric Heyting algebra) in connection with his solution of the problem “does every Heyting algebra occur as Sub(1) in a topos?”. In this talk we focus on the relationship between hochas and toposes: we show that there is an equivalence between (finitary) hochas and toposes satisfying a natural “minimality” condition, and in particular that the category of finitary hochas is nothing other than the ind-completion of the dual of the free topos.
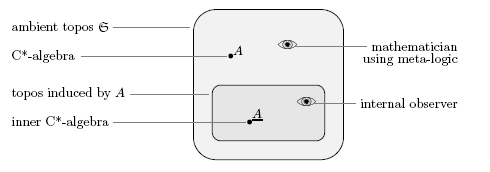
Bas Spitters: Bohrification: topos theory and quantum theory
The recently developed technique of Bohrification associates to a (unital) -algebra
- the Kripke model, a presheaf topos, of its classical contexts
- in this Kripke model a commutative -algebra, called the Bohrification
- the spectrum of the Bohrification as a locale internal in Kripke model.
We will survey this technique, provide a short comparison with the related work by Isham and co-workers, which motivated Bohrification, and use sites and geometric logic to give a concrete external presentation of the internal locale. The points of this locale may be physically interpreted as (partial) measurement outcomes.

Re: The Scottish Category Theory Seminar
New news: Benno van den Berg will give a series of three lectures on algebraic set theory at Strathclyde the day after our meeting, Friday 3 December.
This isn’t part of the Scottish Category Theory Seminar itself, but it’s an extra reason to make the trip. Details will appear, I believe, on the Seminar web page.