Girih by Egan
Posted by John Baez
Check out Greg Egan’s new Girih applet that generates quasiperiodic tilings with ten-fold rotational symmetry, using a method called "inflation". You’ll see patterns like this, that keep zooming in endlessly…
Though quasiperiodic tilings are often attributed to Penrose, in fact they were discovered in the 15th century by the Timurids: a dynasty of Mongol origin who ruled over a large empire in Central Asia, Persia and Mesopotamia. This fact was rediscovered by Peter Lu and Jacob Steinhardt. Egan saw designed related to the above one on a mosque in Isfahan during a trip to Iran. What was he doing in Iran? Researching his latest novel, Zendegi.
“Girih”, or “strapwork”, is the name for the braid-like patterns that the Timurids used to decorate their designs. Here is a set of five tiles used to make designs with 5- or 10-fold quasisymmetry:


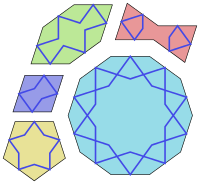
quasicrystals and CQG? Re: Girih by Egan
Beautiful when static, more so when dynamic. The Math journals have been tracking the story. It seems unlikely that anyone in the 15th century saw these in terms of 2-D slices through 4-D or higher periodic tessellations, nor understood quasicrystals. Nor, for that matter, beat Penrose and John Lucas to the punch with belief that deterministic non-algorithmic processes may come in play in the quantum mechanical wave function reduction, and may be harnessed by the brain. Nor with “correct quantum gravity,” CQG. But if Greg Egan puts that into fiction, I’ll willingly suspend disbelief.