Skip to the Main Content

Note:These pages make extensive use of the latest XHTML and CSS Standards. They ought to look great in any standards-compliant modern browser. Unfortunately, they will probably look horrible in older browsers, like Netscape 4.x and IE 4.x. Moreover, many posts use MathML, which is, currently only supported in Mozilla. My best suggestion (and you will thank me when surfing an ever-increasing number of sites on the web which have been crafted to use the new standards) is to upgrade to the latest version of your browser. If that's not possible, consider moving to the Standards-compliant and open-source Mozilla browser.

November 29, 2008

This Week’s Finds in Mathematical Physics (Week 272)

Posted by John Baez

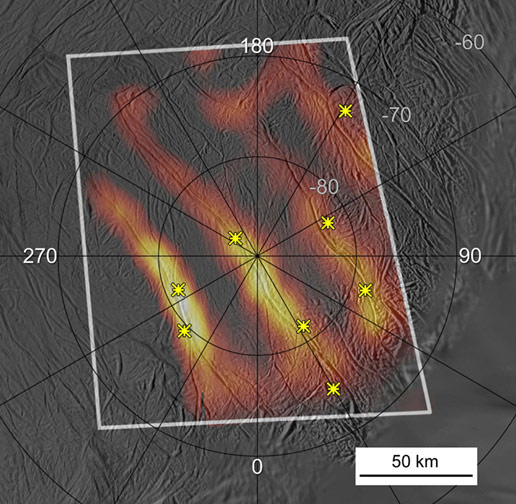
In week272 of This Week’s Finds, see what the Cassini probe saw as it shot through the icy geysers of Enceladus:

See what happens when the Io flux tube hits Jupiter. Learn two new properties of the number 6. And discover the wonders of standard Borel spaces, commutative von Neumann algebras, and Polish groups!

I often dislike artist’s visualizations of scenes from outer space. But this one I like. It’s Cassini whizzing through the Enceladus plumes, as drawn by Karl Kofoed.


Posted at November 29, 2008 4:23 AM UTC

TrackBack URL for this Entry:   https://golem.ph.utexas.edu/cgi-bin/MT-3.0/dxy-tb.fcgi/1864



19 Comments & 0 Trackbacks

Re: This Week’s Finds in Mathematical Physics (Week 272)

A small correction: not every metrizable space embeds in the Hilbert cube (the simplest counterexample being an uncountable discrete space). A topological space is separable and metrizable iff it embeds in the Hilbert cube.

Posted by: Eric on November 29, 2008 3:56 PM | Permalink | Reply to this

Re: This Week’s Finds in Mathematical Physics (Week 272)

Thanks, I’ll fix that. I actually knew that…

Posted by: John Baez on November 29, 2008 4:58 PM | Permalink | Reply to this

Re: This Week’s Finds in Mathematical Physics (Week 272)

Ted Nitz suggested an improvement. This is a better way of listing the probabilities that various finite simple groups are generated by 2 randomly chosen elements:

PSL(2,4)=PSL(2,5)=A 5PSL(2,4) = PSL(2,5) = A_5 has probability 19/30

PSL(2,7)=PSL(3,2)PSL(2,7) = PSL(3,2) has probability 19/28

PSL(2,8)PSL(2,8) has probability 71/84

PSL(2,9)=A 6 PSL(2,9) = A_6 has probability 53/90

PSL(2,11)PSL(2,11) has probability 127/165


I wish someone would tell me the probabilities for

PSL(2,3)=A 4PSL(2,3) = A_4

and

PSL(4,2)=A 9PSL(4,2) = A_9

just so I’d have an excuse to list all the unexpected isomorphisms between alternating groups (A nA_n’s) and projective special linear groups (PSL’s).

Of course it should be a 10-minute calculation for A 4A_4, so I would do it if I weren’t so darn lazy… but A 9A_9 sounds like serious work.

By the way: each of these isomorphisms makes a wonderful story in itself - but not for today! If you want to know these stories, try the first of Conway’s “Three Lectures on Exceptional Groups” from his book with Sloane on Sphere Packings, Lattices and Groups. Also try week79, to see how these stories are related to Galois’ fatal duel and the buckyball.

Posted by: John Baez on November 29, 2008 6:52 PM | Permalink | Reply to this

Re: This Week’s Finds in Mathematical Physics (Week 272)

I think PSL(4,2) is isomorphic to A_8 rather than A_9. Let me also mention the isomorphism PSL(2,2)=S_3 even if it is not simple nor alternating.

By the way, is S_6 the automorphism group of a finite group?

Posted by: Benoit on December 1, 2008 6:27 AM | Permalink | Reply to this

Re: This Week’s Finds in Mathematical Physics (Week 272)

Enceladus is the white blog in the middle of the ring.

And there I was hoping that the Saturnian system was blog-free.

Posted by: Greg Egan on November 29, 2008 11:26 PM | Permalink | Reply to this

Re: This Week’s Finds in Mathematical Physics (Week 272)

My fingers wrote it, not me.

Posted by: John Baez on November 30, 2008 12:51 AM | Permalink | Reply to this

Re: This Week’s Finds in Mathematical Physics (Week 272)

I get a probability of 2/3 for two randomly chosen elements of A 4A_4 generating the group. (For anyone else tackling this, the probabilities refer to two independent random choices, not a random choice of a distinct pair of elements; I initially assumed the latter and got horribly confused.)

Posted by: Greg Egan on November 30, 2008 1:17 AM | Permalink | Reply to this

Re: This Week’s Finds in Mathematical Physics (Week 272)

Ted Nitz wrote a little sage program which also got 2/3 for A4 — see the Addendum to week272. His program is still chugging away on A9. I can imagine more efficient programs… but I’m sure we’ve all got more fun things to do with our time.

Posted by: John Baez on November 30, 2008 7:06 AM | Permalink | Reply to this

Re: This Week’s Finds in Mathematical Physics (Week 272)

I’m running some Mathematica code myself, but I’ll mention my assumptions now in case anyone cares to comment on them.

Given some g∈A 9g\in A_9, I’m assuming that the count of elements h∈A 9h\in A_9 such that <{g,h}>=A 9\lt\{g,h\}\gt = A_9 depends only on the cycle structure of gg, i.e. the numbers of cycles of various lengths in its decomposition into disjoint cycles. That assumption seems pretty solid in the case of the symmetric groups, because two elements with the same cycle structure belong to the same conjugacy class; I think it’s also correct for the alternating groups – despite the fact that elements with the same cycle structure need not be in the same conjugacy class – but if I’m kidding myself about that, now would be a good time for someone to tell me!

I count just 16 different cycle structures for A 9A_9, and I just check one representative gg of each.

And for each gg, rather than checking whether <{g,h}>=A 9\lt\{g,h\}\gt = A_9 for every single h∈A 9h\in A_9, I’m using the fact that if <h 1>=<h 2>\lt h_1\gt = \lt h_2 \gt then <{g,h 1}>=<{g,h 2}>\lt\{g,h_1\}\gt = \lt\{g,h_2\}\gt. I count 53,426 distinct cyclic subgroups <h>\lt h\gt, and I’m just checking a representative generator of each.

One other optimisation I’m using is to note that if gg and hh share any fixed points then obviously they can’t generate the whole group.

Anyway, I should have an answer within a few hours.

Posted by: Greg Egan on November 30, 2008 10:48 AM | Permalink | Reply to this

Re: This Week’s Finds in Mathematical Physics (Week 272)

I woke up up in the middle of the night and felt the need to check a certain blog entry for posts by sockpuppets. I found this instead, which in a way is worse, since now I’ll stay awake thinking about whether two elements A nA_n with the same cycle structure necessarily partake in the same number of pairs that generate the whole group.

This is exactly what I meant by saying ‘I can imagine more efficient programs’. But, I’d foolishly not realized that elements with the same cycle structure needn’t be conjugate in A nA_n. (The appearance of wisdom is often preserved by making short, cryptic remarks instead of more detailed comments that reveal the flaws in ones thinking.)

How about this: conjugation by any element of S nS_n acts as a (possibly outer) automorphism of A nA_n. Thus, for any two elements g,g′g, g' in A nA_n with the same cycle structure there’s an automorphism f:A n→A nf: A_n \to A_n with f(g)=g′f(g) = g'. Finally, whenever g,g′g,g' are two elements for which such an automorphism exists, the number of elements hh such that ⟨{g,h}⟩\langle \{ g, h \} \rangle is the the whole group equals the number of elements h′h' such that ⟨{g′,h′}⟩\langle \{ g', h' \}\rangle is the whole group. Doesn’t that seem right?

Back to sleep.

Posted by: John Baez on November 30, 2008 12:43 PM | Permalink | Reply to this

Re: This Week’s Finds in Mathematical Physics (Week 272)

Doesn’t that seem right?

Yes, that’s how I was thinking of it myself, but I was worried I might just have talked myself into believing it made sense when it didn’t (having not had much sleep last night). Sorry to have provided fuel for your insomnia!

My algorithm does give the right answers for A 4A_4, A 5A_5 and A 6A_6, which is a good sign, though of course subject to the risk of unanticipated complications being more likely to show up for larger nn. It’ll be good to have a cross-check from someone else, eventually.

Posted by: Greg Egan on November 30, 2008 1:07 PM | Permalink | Reply to this

Re: This Week’s Finds in Mathematical Physics (Week 272)

I get the following results for the probability that two independently chosen elements of the group generate the entire group:

P(A 1)=1P(A_1) = 1

P(A 2)=1P(A_2) = 1

P(A 3)=8/9≈0.8889P(A_3) = 8/9 \approx 0.8889

P(A 4)=2/3≈0.6667P(A_4) = 2/3 \approx 0.6667

P(A 5)=19/30≈0.6333P(A_5) = 19/30 \approx 0.6333

P(A 6)=53/90≈0.5889P(A_6) = 53/90 \approx 0.5889

P(A 7)=229/315≈0.7270P(A_7) = 229/315 \approx 0.7270

P(A 8)=133/180≈0.7389P(A_8) = 133/180 \approx 0.7389

P(A 9)=15403/18144≈0.8489P(A_9) = 15403/18144 \approx 0.8489

Adam, thanks for the tip about the order-2 elements.

Posted by: Greg Egan on December 1, 2008 2:45 AM | Permalink | Reply to this

Re: This Week’s Finds in Mathematical Physics (Week 272)

Thanks for the results, Greg! I’ve put them into a new improved table in week272, and put a bit of the tale behind this table in the Addendum.

Posted by: John Baez on December 1, 2008 3:38 AM | Permalink | Reply to this

Re: This Week’s Finds in Mathematical Physics (Week 272)

I agree with the argument. It seems only to rely on the fact that the homomorphic image of a group given by a set of generators will have as its image a group generated by the image of the generators.

I’m not sure how much it will help the computations, but if g is an element of order 2, then you don’t need to check it against any other element of order 2 as this will always give a dihedral group.

Posted by: Adam Glesser on December 1, 2008 2:09 AM | Permalink | Reply to this

Re: This Week’s Finds in Mathematical Physics (Week 272)

I added a nice picture of the temperature profile of the four tiger stripes, with approximate locations of active geysers:

You can see why Damascus Sulcus is the most active, followed by Baghdad Sulcus, Cairo Sulcus and Alexandria Sulcus as we move from left to right.

Also, George Musser passed me a great Scientific American article by Carolyn Porco, where she explains some truly exciting hypotheses about why the south pole of Enceladus is so hot. I’ll have to talk about these sometime.

You can see a cute photo of Carolyn Porco and the rest of the Cassini Imaging Team here. She’s the one at far right.

Posted by: John Baez on December 1, 2008 4:18 AM | Permalink | Reply to this

Re: This Week’s Finds in Mathematical Physics (Week 272)

The Volkswagen beetle is missing, pity…

Posted by: Scott Carter on December 1, 2008 3:14 PM | Permalink | Reply to this

Re: This Week’s Finds in Mathematical Physics (Week 272)

I used to live down that road! I must admit that the fun of seeing people do that did fade slightly after a year of being delayed by it on the bus… but still, nice photo!

Posted by: Jamie Vicary on December 1, 2008 4:14 PM | Permalink | Reply to this

Re: This Week’s Finds in Mathematical Physics (Week 272)

This picture by Ron Miller has its own charm — the people are there to indicate the scale, but it reminds me of the cover of an old SF book:

Posted by: John Baez on December 1, 2008 4:27 AM | Permalink | Reply to this

6 is sexy;Re: This Week’s Finds in Mathematical Physics (Week 272)

Interestingly, a higher proportion of Bernoulli denominators equal 6 than any other value (Sunseri 1980), and the fraction of even Bernoulli numbers with denominator 6 is close to 1/6 (Erdos and Wagstaff 1980).

See the histogram about this at:

Weisstein, Eric W. “Bernoulli Number”, From MathWorld–A Wolfram Web Resource

Posted by: Jonathan Vos Post on December 2, 2008 6:43 AM | Permalink | Reply to this

Post a New Comment