Classical vs Quantum Computation (Week 18)

March 15, 2007

Classical vs Quantum Computation (Week 18)

Posted by John Baez

$MathML-enabled post (click for more details).$

Today we had our last class on Classical vs Quantum Computation for this quarter:

Week 18 (Mar. 15) - 2-categories from typed λ-calculi, continued. The Church-Rosser theorem. Surface diagrams showing the process of computation. β-reduction as a fold catastrophe. Thom’s ideas on catastrophe theory. Challenge: draw the surface diagram for η-reduction. Which catastrophe does it correspond to? Blog entry.

Supplementary reading:
- Lucien Dujardin, Catastrophe teacher: an introduction for experimentalists.
- Barnaby P. Hilken, Towards a proof theory of rewriting: the simply-typed 2λ-calculus, Theor. Comp. Sci. 170 (1996), 407–444.
- R. A. G. Seely, Weak adjointness in proof theory in Proc. Durham Conf. on Applications of Sheaves, Springer Lecture Notes in Mathematics 753, Springer, Berlin, 1979, pp. 697–701.
- R. A. G. Seely, Modeling computations: a 2-categorical framework, in Proc. Symposium on Logic in Computer Science 1987, Computer Society of the IEEE, pp. 65–71.
- C. Barry Jay and Neil Ghani, The virtues of eta-expansion, J. Functional Programming 1 (1993), 1–19.

Last week’s notes are here; next week’s notes are here.

$MathML-enabled post (click for more details).$

We came pretty close to our goal of explaining how processes of computation are 2-morphisms in a 2-category. Namely, we came close to seeing how for any typed λ-calculus there’s a 2-category with

types as objects,
terms as morphisms,
rewrite rules (ways of simplifying terms) as 2-morphisms.

We saw how to draw these 2-morphisms as surfaces, and we noticed an intriguing relation to René Thom’s ideas on catastrophe theory: it turned out that the process of ‘applying a function to its argument’ gives a surface with the simplest sort of catastrophe — a fold catastrophe:

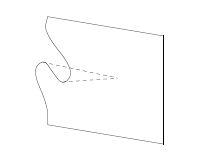
We did not reach our goal of proving that the 2-category we got is a ‘cartesian closed 2-category’. In fact, we didn’t even define that concept! Nor did we get around to generalizing all this to the non-cartesian — or roughly speaking, ‘quantum’ — context.

Today’s session was a bit sad, because it’s the last one my student Mike Stay will attend. He’s the one who turned my interest in categories and computation from a hobby to something a bit more than a hobby, by coming to U.C. Riverside with a master’s in computer science and wanting to work on categories and quantum computation. Unfortunately, he couldn’t earn enough money here to support his family, so he took a job at Google, and he’s leaving town this weekend. Luckily, his skills in cryptography will now let him earn more than I do! I’m hoping he becomes a bigshot at Google and sets up a little n-category research group.

Right now we’re writing an expository paper on logic, computation, categories and Feynman diagrams, for a book Bob Coecke is editing. Google has a nice policy of letting their employees spend one day a week on projects of their own choosing. So, we’ll keep working away — but it won’t be the same. I may or may not keep the Classical vs Quantum Computation seminar going in the Spring quarter: my other students are working on other stuff!

Posted at March 15, 2007 9:36 PM UTC

TrackBack URL for this Entry: https://golem.ph.utexas.edu/cgi-bin/MT-3.0/dxy-tb.fcgi/1205

16 Comments & 3 Trackbacks

Read the post Classical vs Quantum Computation (Week 17)
Weblog: The n-Category Café
Excerpt: String worldsheets illustrating processes of computation!
Tracked: March 15, 2007 10:48 PM

Read the post Classical vs Quantum Computation (Week 18)
Weblog: The n-Category Café
Excerpt: Surface diagrams showing the process of computation.
Tracked: March 15, 2007 10:50 PM

Re: Classical vs Quantum Computation (Week 18)

I was under the impression that Whitney, not Thom, discovered the fold map, and more generally classified singularities of 2-dimensional maps (i.e. maps R² → R²).

(I was also under the impression that since the 1980s there’s a rule against calling these things “catastrophes,” but maybe the backlash has died down enough by now.)

Posted by: Changbao on March 16, 2007 12:29 AM | Permalink | Reply to this

Re: Classical vs Quantum Computation (Week 18)

$MathML-enabled post (click for more details).$

Thanks for the info about Whitney!

I know there was a harsh reaction against the inflated rhetoric about catastrophe theory that was so common after René Thom’s Structural Stability and Morphogenesis and Semiophysics came out.

However, it’s precisely one of Thom’s dangerously broad claims that I wanted to take up here, namely that verbs correspond to catastrophes. This is a relation between syntax and differential topology — and it’s precisely this sort of relation we’re seeing when we use surface diagrams to represent processes of computation in the 2-category coming from a typed λ-calculus!

Of course in $n$ -category theory we say ‘object’ instead of ‘noun’, ‘morphism’ instead of ‘verb’ — and we can go further and talk about 2-morphisms, etc. Thom didn’t think in terms of $n$ -categories, but that needn’t stop us.

By following some systematic rules, we saw in class that the process of evaluating a function, or more precisely the 2-morphism ‘β-reduction’, corresponds to a fold catastrophe! And this is just the tip of the iceberg — further thought along these lines quickly takes us to the swallowtail singularity, and beyond.

So, something big is going on, and the person to blame for these dangerously sexy big ideas is Thom, not Whitney.

Of course, some people got carried away with catastrophe theory in rather silly ways. But it would also be silly not to mention it when some of Thom’s ideas are getting realized in a very precise way.

Posted by: John Baez on March 16, 2007 3:17 AM | Permalink | Reply to this

Re: Classical vs Quantum Computation (Week 18)

$MathML-enabled post (click for more details).$

So $\beta$ -reduction and ‘The day ends’ share a common structure.

Returning to precise disciplines, there remains the small problem of relating this to fundamental $n$ -categories of statified spaces, the kind of thing we talked about back here. Can one see $\beta$ -reduction in terms of a stratified space?

Posted by: David Corfield on March 16, 2007 3:28 PM | Permalink | Reply to this

Re: Classical vs Quantum Computation (Week 18)

$MathML-enabled post (click for more details).$

David wrote:

Can one see β-reduction in terms of a stratified space?

That’s a fun question!

I hope stratified spaces give $n$ -categories with duals, and there’s some evidence for this. An example is a symmetric monoidal category with duals, as defined below. These are relevant to quantum logic and the ‘quantum λ-calculus’.

Lately I’ve been catching up on the ‘classical λ-calculus’, and today’s class only discussed this. This is all about cartesian closed categories.

So: if we want to relate β-reduction to stratified spaces, it’ll work more smoothly if we consider β-reduction in the quantum λ-calculus!

If we did that, I would not have to draw ‘bubbles’ in my string diagrams and surface diagrams, as I did in today’s notes. For more on the role of these bubbles, read about popping bubbles to reveal the quantum world.

So, anyway, the answer to your question is yes: in the ‘quantum’ case, where we have a symmetric monoidal category with duals $C$ , we should be able to build a stratified space whose fundamental category is $C$ . And then, β-reduction in the corresponding quantum λ-calculus should really be related to fold singularities in a very direct way!

This would be fun to explore. It would really bring out the full content of the word topological.

Some reminders may be helpful, at least for people who are insufficiently fanatical about attending this Café:

Suppose $C$ is a symmetric monoidal category. Then we say:

$C$ is closed if the functor of tensoring with any object $x \in C$ : $a \to x \otimes a$ has a right adjoint, the internal hom $b \to hom(x,b) .$ In other words, we have a natural isomorphism $HOM(x \otimes a, b) \cong HOM(a, hom(x,b)).$ Here HOM denotes the usual set of morphisms from one object to another, while hom is the “internal hom”, which is an object in our category. If the tensor product in $C$ is cartesian, and $C$ is also closed, we call it cartesian closed.
$C$ has duals for objects if it is closed and for any object $x \in C$ there is an object $x^* \in C$ , the dual of $x$ , such that $hom(x,b) \cong x^* \otimes b$ for all $b \in C$ . If $C$ has duals for objects, it’s common for category theorists to say $C$ is compact or compact closed; algebraic geometers say it’s rigid.
$C$ has duals for morphisms if for any morphism $f : a \to b$ there is a morphism $f^\dagger: b \to a$ such that $f^{\dagger \dagger} = f$ $(f g)^\dagger = (g f)^\dagger$ $1^\dagger = 1$ and all the structural isomorphisms (the associator, the left and right unit laws, and the braiding and balancing) are unitary, where a morphism $f$ is unitary when $f^\dagger$ is the inverse of $f$ .
$C$ has duals if it has duals for objects and morphisms. If $C$ has duals, Abramsky and Coecke call it strongly compact closed, while Selinger calls it dagger compact closed.

The category of finite-dimensional Hilbert spaces is symmetric monoidal, and it has duals. The same is true for $n Cob$ , whose morphisms are $n$ -dimensional cobordisms, like this (for $n$ = 2):

$cobordism$

Posted by: John Baez on March 16, 2007 8:04 PM | Permalink | Reply to this

Re: Classical vs Quantum Computation (Week 18)

James Tobias of the English department at UCR came to this class, having seen an announcement for it, and being interested in quantum computation. I warned him that it was the last class of two quarter’s worth of fancy mathematics. Amazingly, he seemed to enjoy or at least tolerate it!

The participants of the class had a short discussion of the etymology of the word ‘catastrophe’. Here’s some followup from Prof. Tobias:

By the way, I also thought that “strophe” was an equivalent of the Latin “trope,” but I was confused between the Latin and Greek. So I looked up the terms in the OED to make sure of the meanings. “Strophe” of “catastrophe” is, as you indicated, “a turning,” so that “catastrophe” is an “overturning” or broadly, a sudden conclusion.

The OED on “strophe”: “Originally the word στροφη, ‘turning’, was applied to the movement of the chorus from right to left, and αντιστροφη [antistrophe], ‘counter-turn’, to its returning movement from left to right; hence these terms became the designations of the portions of the choric ode sung during these movements respectively.”

In these terms, since you so elegantly “fell turning” into your conclusions after the back and forth parsing of functions and diagrams, your talk, including the call and response with your chorus of graduate students, was for this outsider, a very successful catastrophe!

Warmly,

James Tobias

Posted by: John Baez on March 22, 2007 12:11 AM | Permalink | Reply to this

Read the post Cohomology and Computation (Week 19)
Weblog: The n-Category Café
Excerpt: The origins of cohomology in the study of 'syzygies', or relations between relations.
Tracked: April 20, 2007 8:39 PM

Re: Classical vs Quantum Computation (Week 18)

$MathML-enabled post (click for more details).$

I went to a neat talk here at Google yesterday. It was about an interesting paper that says given only the type of a term, you can construct the term of that type that must be there, and also about a Haskell program “Djinn” that “magically” produces the code.

There’s a list of examples and a help file that explains a little bit about how to use it.

It produced code for identity, S and K combinators, first and second projections from a pair, swap, compose, curry, uncurry, bind and return for monads, even call-with-current-continuation, all from just the type information.

I think it also generated the traditional Church-numeral code for zero and plus, but I’m not sure about that.

Posted by: Mike Stay on April 23, 2007 8:03 PM | Permalink | Reply to this

Re: Classical vs Quantum Computation (Week 18)

$MathML-enabled post (click for more details).$

On 4/24/07, John Baez wrote:

Thanks! It’s an interesting paper, but I’ll need to learn about the “polymorphic” lambda-calculus and some other stuff before really appreciating it.

Encapsulation, inheritance and polymorphism are the three things that object-oriented programming brought to imperative languages like C or Fortran.

(Parametric) polymorphism is a second-order concept. It lets you give datatypes as inputs to other datatypes, not just as inputs to function symbols.

For instance, consider lists. A list datatype should have some function symbols that act on it. We’d like to be able to - append an element to the list - project onto the nth element of the list - get the list length - etc.

Notice that I never said what type an element is! In the first-order lambda calculus, I’d have to specify what the output datatype of the projection function symbol is. Here, it shouldn’t matter: the projections should work the same way no matter what the element type is.

The element datatype becomes a parameter in the definition of a list, and we can use the same function symbols on many differently-shaped objects. Thus “parametric polymorphism”.

Posted by: Mike Stay on April 25, 2007 6:09 AM | Permalink | Reply to this

Re: Classical vs Quantum Computation (Week 18)

Silly pedantry: Christopher Strachey at least was thinking about the different kinds of polymorphism that can occur in computer languages in the context of imperative languages before the initial object oriented programming languages became popular.

This doesn’t change your real points of course.

Posted by: dave tweed on April 25, 2007 6:24 AM | Permalink | Reply to this

Re: Classical vs Quantum Computation (Week 18)

Someday I would like to understand polymorphism from a nice category-theoretic point of view. I have a book checked out from the library which claims to handle this using fibered categories… I forget the author and title right now, and it’s back home (I’m in my office).

Posted by: John Baez on May 3, 2007 12:25 AM | Permalink | Reply to this

Re: Classical vs Quantum Computation (Week 18)

Could it be “Categories for Types” by Roy Crole? If not, you might want to try it.

Posted by: Tom Leinster on May 3, 2007 1:37 AM | Permalink | Reply to this

Re: Classical vs Quantum Computation (Week 18)

$MathML-enabled post (click for more details).$

No, it’s not Categories for Types — it’s something more high-powered, or at least more difficult to understand. It’s got a yellow cover, instead of a yellow and blue cover. I’ll say something more useful when I get home.

Perhaps though it would be good for me to look again at Categories for Types. Previously I only paid attention to the chapters on categories with finite products (‘algebraic theories’) and cartesian closed categories (‘the typed lambda-calculus’). There are further chapters that go into more complicated topics. Does it discuss polymorphism?

(By the way, I’ve always found the title Categories for Types amusing. At first it sounds analogous to Topology and Geometry for Physicists. But what sort of person is a ‘type’? Is it like a ‘character’?)

Posted by: John Baez on May 3, 2007 1:53 AM | Permalink | Reply to this

Re: Classical vs Quantum Computation (Week 18)

But what sort of person is a ‘type’?

In French, “type” is roughly equivalent to “guy”, as in “this guy says…”

Posted by: John Armstrong on May 3, 2007 2:31 AM | Permalink | Reply to this

Re: Classical vs Quantum Computation (Week 18)

Sounds like Bart Jacobs’s book.

Posted by: Robin on May 3, 2007 11:20 AM | Permalink | Reply to this

Re: Classical vs Quantum Computation (Week 18)

Yes, it’s Bart Jacob’s Categorical Logic and Type Theory! Thanks. Turns out I’d already returned it to the library…

Posted by: John Baez on May 3, 2007 9:52 PM | Permalink | Reply to this

Re: Classical vs Quantum Computation (Week 18)

$MathML-enabled post (click for more details).$

I just added a bunch more links to 2-categorical aspects of the $\lambda$ -calculus. Most of these are familiar to those in the know, but Paul-André Melliè pointed me to one I’d never seen:

Barnaby P. Hilken, Towards a proof theory of rewriting: the simply-typed 2λ-calculus, Theor. Comp. Sci. 170 (1996), 407–444.

Posted by: John Baez on July 18, 2007 12:07 PM | Permalink | Reply to this

Re: Classical vs Quantum Computation (Week 18)

Please pardon this interruption, but this brief experimental paper by Dolev and Elitzur which was also published in an edited book shows the non-sequential behavior of the wavefunction in QM. The overall result of this paper is Lorentz-invariant, but still with Bell-like correlations and, as the authors conclude, this result appears to transcend ordinary concepts of probability theory, causality, space and time:

http://arxiv.org/abs/quant-ph/0102109

I have previously suggested that this non-sequential behavior of the wavefunction might have something to do with the speed-up of quantum computation over classical computation. Do you see any way to relate this experimental finding of Dolev and Elitzur to the categories Hilb or nCob? Thanks.

Posted by: Charlie Stromeyer on June 29, 2009 10:00 PM | Permalink | Reply to this

The n-Category Café

Skip to the Main Content

March 15, 2007