Musings

Forward scattering produced the bounds $$\array{\arrayopts{\colalign{right left}} \bar \ell_1+2 \bar \ell_2&\geq \frac{1}{32} (-36+9 \pi )\\ \bar \ell_2&\geq \frac{1}{48} (-92+39 \pi )\\ \bar \ell_1+3 \bar \ell_2&\geq 0.911166 }$$ Theoretically, this was notable because the shape of the allowed region differed from that predicted by the classical superluminality analysis, which can also be thought of as modified classical propagation resulting from (tree-level) forward scattering off a nontrivial background field.

The new, stronger bounds are $$\array{\arrayopts{\colalign{right left}} \bar \ell_1+2 \bar \ell_2&\geq 157/40\\ \bar \ell_2&\geq 27/20\\ \bar \ell_1+3 \bar \ell_2 &\geq 211/40. }$$ Unlike the previous case, the 3rd bound is redundant to the other two. A comparison of the old and new bounds can be seen in the figure below.

The region allowed by the dispersion relation analysis. Forward scatter dispersion relations exclude the crimson and burnt orange regions. The new bounds exclude the light blue region as well.

Theoretically, you might not find the new bounds all that interesting an improvement over the old ones. But, when you compare them with what might be measured experimentally at the ILC, the new, tighter bounds become somewhat more interesting experimentally.

There’s more work to be done, but one can kinda get a rough idea by comparing our bounds with the following graph from Boos et al. To make the comparison, $\alpha_4 \sim \overline{\ell}_2/192\pi^2$ $\alpha_5 \sim \overline{\ell}_1/384\pi^2$.

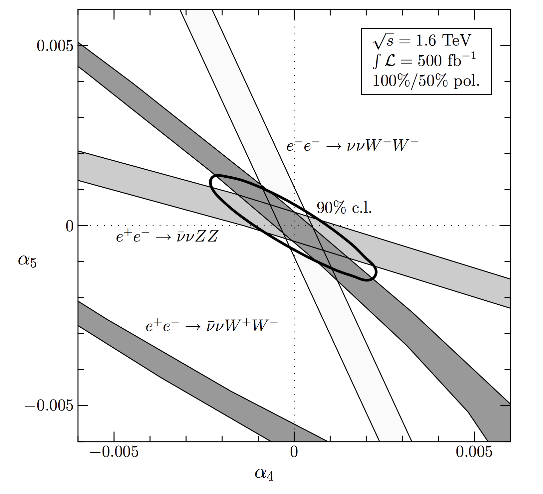
1-$\sigma$ exclusion contours for all three processes in the $\alpha_4/\alpha_5$ plane, based on the hypothesis $\alpha_4=\alpha_5=0$. All cuts have been applied and detection efficiencies are included. The closed contour curve is the 90% exclusion limit obtained by combining the $e^+e^-\to \bar\nu\nu W^+W^-$ and $e^+e^-\to \bar\nu\nu ZZ$ channels. (from Boos et al)

What one would like to show, for instance, is that a measurement which yielded that 90% CL ellipse implies a violation of our bounds …