Musings

Blackhole Production

One (unlikely, but) exciting prospect is that, if there are large extra dimensions and TeV-scale gravity, one would produce blackholes at the LHC. Giddings and Eardley’s calculation of semiclassical blackhole formation in high energy scattering leads one to believe that, if the fundamental Planck scale is low enough (say, $M_D\sim 3\text{TeV}$) and the number, $n$, of large extra dimensions large enough, one ought to see copious numbers of blackholes ($\sim 10^3$/year for $n=3$, and a luminosity of $10^{33}\text{cm}^{-2}s^{-1}$) at the LHC.

This would be incredibly dramatic. But, as Yoshino and Nambu showed, there’s an important effect which needs to be included, namely that some significant fraction of the center-of-mass energy is radiated away before the blackhole forms. When you include this inefficiency, the production rate goes way down (because we need to be further out on the tail of the parton distribution function).

Anchordoqui, Feng, Goldberg and Shapere have looked at the numbers for the LHC, and compared them with what can be seen from cosmic ray observatories. In cosmic ray searches, one can look for quasi-horizontal showers produced by cosmic ray neutrinos. If the TeV-scale gravity story is correct, blackhole formation dominates the total cross section at high energies. Looking only at quasi-horizontal showers minimizes the background from other sources, so this provides a fairly clean, dramatic signal.

Cosmic ray neutrinos have some advantages over the LHC.

1. You pay the price of only one parton distribution function, instead of two.
2. AGASA is already taking data, and Auger will be soon.

By the time LHC turns on, they will have accumulated several more years of data. Either they will have seen blackholes, or they will have set limits which leave the LHC only a very narrow window for discovery.

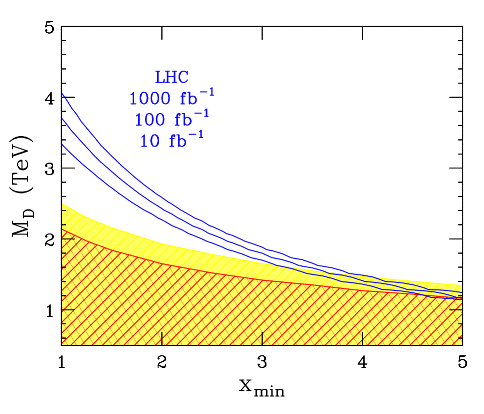
The discovery reaches for the LHC (solid) for 3 different integrated luminosities and $n = 6$ extra dimensions. Also shown is the region of parameter space which can be excluded at 95% CL if no neutrino showers mediated by BHs are observed in 5 years at the PAO. The shaded (cross-hatched) region assumes 2 SM neutrino + 0 (10) hadronic background events. $M_D$ is the fundamental Planck scale, and $x_{\text{min}}$ is the mass (in units of $M_D$) of the smallest mass blackhole which can be cleanly distinguished. Ten years of the LHC running at $10^{34}$ represents an integrated luminosity of 1000 fb^-1 (from Anchordoqui et al).

There is, at least, one loophole in this analysis. Yoshino and Nambu only computed a lower bound on $M_{BH}/\sqrt{s}$. But it seems unlikely that the actual ratio will be significantly larger than this and — in any case — this affects both cosmic ray and LHC searches. Also, the flux of cosmic ray neutrinos isn’t really known but it is, at least, bounded below by that due to pion production from cosmic ray protons.

Now, I don’t think either Auger or LHC will see blackholes. But I was surprised to learn how competitive high energy cosmic ray observatories have become in doing particle physics.