The Riemann Hypothesis Says 5040 is the Last

July 6, 2019

The Riemann Hypothesis Says 5040 is the Last

Posted by John Baez

$MathML-enabled post (click for more details).$

There are many equivalent ways to phrase the Riemann Hypothesis. I just learned a charming one from this fun-filled paper:

Jeffrey Lagarias, Euler’s constant: Euler’s work and modern developments, Bull. Amer. Math. Soc. 50 (2013), 527–628.

$MathML-enabled post (click for more details).$

Let $\sigma(n)$ be the sum of the divisors of $n$ , for example

$\sigma(12) = 1 + 2 + 3 + 4 + 6 + 12 = 28$

In 1984 Guy Robin showed that the Riemann Hypothesis is true if and only if

$\frac{\sigma(n)}{n \ln (\ln n)} \; < \; e^\gamma$

for all $n > 5040$ , where $\gamma$ is Euler’s constant

$\begin{array}{ccl} \gamma &=& \displaystyle{ \lim_{n \to \infty} \left( \sum_{i = 1}^n \frac{1}{i} - \int_1^n \frac{d x}{x} \right)} \\ \\ &=& 0.5772156649015328606\dots \end{array}$

What makes this especially tantalizing is that in 1913 Gronwall showed that for any $\epsilon > 0$ ,

$\frac{\sigma(n)}{n \ln (\ln n)} \; < \; e^\gamma + \epsilon$

except for finitely many $n$ . He did this using the Prime Number Theorem.

What’s the deal with 5040? Well, obviously, the sum of the divisors of this number is big compared to $n \ln(\ln n)$ .

In fact, the only known natural numbers $n$ with

$\frac{\sigma(n)}{n \ln (\ln n)} \; \ge \; e^\gamma$

are

$3, 4, 5, 6, 8, 9, 10, 12, 16, 18, 20, 24, 30, 36, 48, 60,$ $72, 84, 120, 180, 240, 360, 720, 840, 2520, \; and\; 5040$

(I’m leaving $1$ and $2$ off this list because $\ln(\ln n)$ is funny for these.)

If there’s any other natural number with this property, the Riemann Hypothesis is false. If there’s not, it’s true!

In fact, Robin showed that if the Riemann Hypothesis is false there are infinitely many natural numbers with this property.

On Twitter, Nicolas Tessore kindly graphed the function $\sigma(n)/(n \ln(\ln n))$ for us:

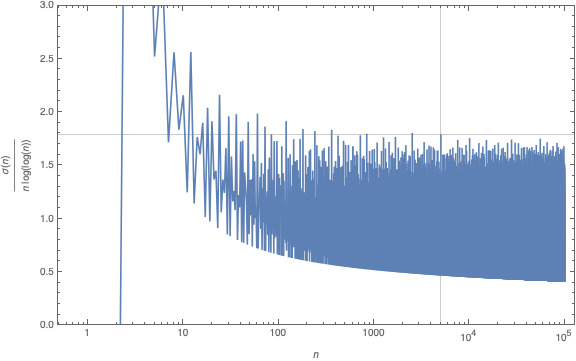
You can see 5040 there, poking its head up, looking to the right, saying “Is there anyone out there as tall as me? Or almost as tall as me?”

Somehow this makes the Riemann Hypothesis very vivid to me.

Posted at July 6, 2019 12:39 PM UTC

TrackBack URL for this Entry: https://golem.ph.utexas.edu/cgi-bin/MT-3.0/dxy-tb.fcgi/3125

15 Comments & 1 Trackback

Re: The Riemann Hypothesis Says 5040 is the Last

$MathML-enabled post (click for more details).$

Some calculations, just for fun.

$\sigma_1(5040) = 19344$

$5040 \ln(\ln 5040) = 10800.83063291229282848974010\dots$

$\frac{\sigma_1(5040)}{5040 \ln(\ln 5040)} = 1.7909733665348811333619013505910 \dots$

$e^\gamma = 1.781072417990197985236504103107 \dots$

Posted by: John Baez on July 6, 2019 2:15 PM | Permalink | Reply to this

Re: The Riemann Hypothesis Says 5040 is the Last

$MathML-enabled post (click for more details).$

I’m curious: what’s the largest known value of

$\frac{\sigma_1(n)}{n \ln(\ln n)}$

for $n > 5040$ ?

Posted by: John Baez on July 6, 2019 2:30 PM | Permalink | Reply to this

Re: The Riemann Hypothesis Says 5040 is the Last

$MathML-enabled post (click for more details).$

I’ve no idea what the official known answer may be – but running this for $n=1$ to $n=10^6$ and searching for values > 1.7, I get the following list of 21 cases. Each is an integer multiple of 2520, and the largest value (for the range up to $n=10^6$ ) is $\approx 1.7558$ , where $n=10080$ .

Each triple below has the form

$(n, n/2520, \frac{\sigma_1(n)}{n ln(ln(n))})$

(where the final term is larger than 1.7). I forgot how to write a table in xhtml…

(7560, 3, 1.739917)

(10080, 4, 1.755814)

(12600, 5, 1.709536)

(15120, 6, 1.738559)

(20160, 8, 1.713811)

(25200, 10, 1.712482)

(27720, 11, 1.742537)

(30240, 12, 1.713954)

(32760, 13, 1.708297)

(55440, 22, 1.751247)

(65520, 26, 1.717889)

(83160, 33, 1.712110)

(110880, 44, 1.734849)

(131040, 52, 1.702694)

(166320, 66, 1.726929)

(221760, 88, 1.708246)

(277200, 110, 1.711244)

(332640, 132, 1.716097)

(360360, 143, 1.711872)

(554400, 220, 1.702593)

(720720, 286, 1.733065)

Posted by: Jeff Ketland on July 8, 2019 1:28 AM | Permalink | Reply to this

Re: The Riemann Hypothesis Says 5040 is the Last

$MathML-enabled post (click for more details).$

Thanks, that’s very interesting! As Mike reminded us, Gronwall actually showed that

$\limsup_{n\to\infty} \frac{\sigma(n)}{n \ln(\ln n)} = e^\gamma$

so there must be infinitely many choices of $n$ that make $\sigma(n)/(n \ln(\ln n)) > 1.78$ , but your winner is $1.751247$ . I wonder what the $n$ with really large values of $\sigma(n)$ are like. I wonder if anyone has put a lot of work into seeking them.

Posted by: John Baez on July 11, 2019 7:18 AM | Permalink | Reply to this

Re: The Riemann Hypothesis Says 5040 is the Last

$MathML-enabled post (click for more details).$

On Twitter, I laid down the challenge to find a natural number $n \, > \, 5040$ with

$\frac{\sigma(n)}{n \ln(\ln(n))} \; >\; 1.781$

Gro-Tsen replied:

The first number I could find beyond 10080 which does better than it is

8201519488959040182625924708238885435575055666675808000

which gives 1.757183 (I’m not claiming there’s nothing in between).

I don’t think it’s computationally feasible to find a number attaining 1.781. I found one which does 1.777: namely,

$2^13 \times 3^8 \times 5^5 \times 7^4 \times 11^3 \times 13^3 \times 17^3 \times 19^2 \times 23^2 \times$ $29^2 \times 31^2 \times 37^2 \times 41^2 \times 43^2 \times 47^2 \times 53^2 \times 59^2 \times 61^2$

times the product of all primes between 67 and 2383 inclusive, or approximately 1.978330464193× $10^1049$ , having a score of about 1.77700981. I can do better, but the score improves so much slower each time.

And here’s the Sage code I used for the computation: code.

Also, googling the number

8201519488959040182625924708238885435575055666675808000

from a few tweets up, I found that the OEIS had got there before me (of course!): A217867.

Posted by: John Baez on July 13, 2019 10:22 AM | Permalink | Reply to this

Re: The Riemann Hypothesis Says 5040 is the Last

$MathML-enabled post (click for more details).$

Yes, I agree, that feels much more concrete and “related to positive integers” than a statement about zeros of the zeta function.

The Wikipedia page about 5040 informs me that in fact it’s known that

$\limsup_{n\to \infty} \frac{\sigma(n)}{n\ln\ln n} = e^\gamma.$

Gronwall’s result as you quoted it is essentially the statement that this limsup is less than or equal to $e^\gamma$ . Knowing that the limsup is actually equal to $e^\gamma$ makes this property of 5040 even more vivid for me; it means that even if the Riemann hypothesis is true, then there must nevertheless be arbitrarily large natural numbers such that $\frac{\sigma(n)}{n\ln\ln n} \gt e^\gamma - \varepsilon$ , for any $\varepsilon\gt 0$ .

Wikipedia also informs me — before getting around to number theory — that Plato believed 5040 was the ideal number of citizens for a city-state because it can be divided up in so many different ways. Maybe Plato believed in the Riemann hypothesis.

Posted by: Mike Shulman on July 6, 2019 2:41 PM | Permalink | Reply to this

Read the post the Riemann hypothesis and 5040
Weblog: neverendingbooks
Excerpt: Yesterday, there was an interesting post by John Baez at the n-category cafe: The Riemann Hypothesis Says 5040 is the Last. The 5040 in the title refers to the largest known counterexample to a bound for the sum-of-divisors function \[ \sigma(n) = \sum...
Tracked: July 7, 2019 1:17 PM

Re: The Riemann Hypothesis Says 5040 is the Last

$MathML-enabled post (click for more details).$

Since you just learned about this criteria, maybe you had not seen this interesting attempt on MO to find a quantum version.

Maybe there’s a great categorification to be found…

Posted by: jon on July 7, 2019 3:25 PM | Permalink | Reply to this

Re: The Riemann Hypothesis Says 5040 is the Last

$MathML-enabled post (click for more details).$

There seems rather less to that “QRH” on MathOverflow than meets the eye. Indeed that question seems to fit a pattern from that user of wanting to shoehorn subfactors into everything…

Posted by: Yemon Choi on July 8, 2019 7:04 AM | Permalink | Reply to this

Re: The Riemann Hypothesis Says 5040 is the Last

$MathML-enabled post (click for more details).$

Just out of curiosity did you just take a few of the factors of 5040 to make this analysis?

Apparently you skipped 7 and all it’s multiples that are factors of 5040.

7, 14, 21,28,35,42,56,63,70,84,105,112,126,140,168,210,252,280,315,336,420,504,560,630,1008,1260,1680

I skipped 840,2520 and 5040 because you had them in your list.

Kind regards,

Eduardo

Posted by: Eduardo Calero on July 7, 2019 8:48 PM | Permalink | Reply to this

Re: The Riemann Hypothesis Says 5040 is the Last

$MathML-enabled post (click for more details).$

For $n=7$ , $\frac{\sigma_1(n)}{n ln(ln(n))} \approx 1.716698$ . This is smaller than $e^{\gamma}$ . Typing this R code into your R console gives the numbers that John listed above

library(numbers); riem <- function(n) { sum(divisors(n))/(n * log(log(n))) }; L <- unlist(lapply(1:(10^4), riem)); gam <- 0.5772156649015328606; const <- exp(gam); which(L > const);

Posted by: Jeff Ketland on July 7, 2019 11:29 PM | Permalink | Reply to this

Re: The Riemann Hypothesis Says 5040 is the Last

$MathML-enabled post (click for more details).$

Or, for a Python version (3 lines, only the basic math library required):

from math import *

exp_gamma = exp(0.57721566490153286)

[n for n in xrange(2, 6000) if sum([m for m in xrange(1, n+1) if n % m == 0]) / (n * log(log(n))) > exp_gamma]

Posted by: Blake Stacey on July 10, 2019 7:43 PM | Permalink | Reply to this

Re: The Riemann Hypothesis Says 5040 is the Last

$MathML-enabled post (click for more details).$

Curious indeed. Just for fun one can relate such numbers to coefficients of the theta function of the E8 lattice.

$\Theta_{\Gamma_8}(\tau)=1+240 q^2+2160 q^4 + 6720 q^6+...$

For example,

2520-2160=360

and

5040-2160-2160=720

In light of this, the numbers don’t seem too arbitrary.

Looking at the theta function for the Barnes-Wall lattice,

$\Theta_{\Gamma_{16}}(\tau)=1+4320 q^2+61440 q^3+ 522720 q^4 + 2211840 q^5+...$

we notice

5040-4320=720

and 720=3*240, where 240 is the number of $E_8$ roots.

Posted by: Metatron on July 8, 2019 8:27 AM | Permalink | Reply to this

Re: The Riemann Hypothesis Says 5040 is the Last

Great fun! I think it is a matter of throwing enough primes at it… Using the first 250000 primes and the following list of exponents (Haskell syntax, I hope it is obvious):

[24,14,12,10,10,9,9,9,9,8,8,8,7,7,7,6,6,6,6,6,6,5,5,5,5,5,5,5,5,5, 4,4,4,4,4,4,4,4,4,4,4,4] ++ replicate 45 3 ++ replicate 300 2 ++ repeat 1

we get 1.7810074

To maintain good precision, I used exact integer arithmetic as much as possible. The code is here:

https://github.com/jeroennoels/john-baez-challenge/blob/master/src/Challenge.hs

Posted by: Jeroen Noels on July 13, 2019 8:08 PM | Permalink | Reply to this

Re: The Riemann Hypothesis Says 5040 is the Last

$MathML-enabled post (click for more details).$

Wow, this is great!

For anyone not following carefully, Jeroen just met this challenge: he found an integer $n \, > \, 5040$ with

$\frac{\sigma(n)}{n \ln(\ln n))} \; > \; 1.781$

It would be nice if someone who knows Haskell can tweak his program a bit and tell me roughly what his integer is, in scientific notation. It’s bigger than $2^{250000} = 10^{75257}$ , but this is a very crude lower bound.

Posted by: John Baez on July 14, 2019 11:19 AM | Permalink | Reply to this

Re: The Riemann Hypothesis Says 5040 is the Last

$MathML-enabled post (click for more details).$

Greg Egan figured it out: Jeroen’s $n \, > \, 5040$ with

$\frac{\sigma(n)}{n \ln(\ln n))} \; > \; 1.781$

is about

$1.42678 \times 10^{1,519,637}$

Posted by: John Baez on July 14, 2019 2:05 PM | Permalink | Reply to this

The n-Category Café

Skip to the Main Content

July 6, 2019