The n-Category Café

This first article is inspired by the paper A finite presentation of CNOT-dihedral operators by Matthew Amy, Jianxin Chen and Neil J. Ross. The result of the paper, existence and uniqueness of a normal form for a fragment of quantum computation, was obtained by the authors by observing an interesting interplay between two languages: the representation of unitary quantum gates as circuits in a symmetric monoidal groupoid, and their description in terms of ‘phase polynomials’.

In this blog post, we add a third language to the ones introduced in the paper, the ZX-calculus. This, inter alia, serves the purpose of putting the work done in the paper into a broader context. On the one hand, we use the ZX calculus to develop an intuition for the relations between unitary gates exposed in the paper, while on the other hand we discuss how the phase polynomial formalism can be imported into the ZX calculus to obtain rewrite strategies for circuit optimization.

Introduction

Quantum computer science studies how to use the properties of quantum mechanical systems for designing algorithms which outperform classical computers. To reason about quantum computation, it is useful to represent algorithms as circuit diagrams. These consist of two basic components. Each wire of the circuit diagram represents a qubit, whose states are (normalised) vectors in a two-dimensional complex Hilbert space, i.e. points on the Bloch sphere. Wires are connected to boxes, which represent operations that can be performed on qubits. These are unitary linear maps, i.e. reversible maps which send points on the Bloch sphere to points on the Bloch sphere, and they are referred to as gates by analogy with classical computation.

A commonly studied unitary fragment of quantum circuits is known as Clifford+T, and it is generated by the gates $C N O T$ (controlled not), $T$ (rotation by $\frac{\pi}{4}$ about the Z axis) and $H$ (the Hadamard gate, corresponding to the rotation which interchanges the Z and X axes on the Bloch sphere). What makes this gate set of particular interest is that while it is finitely generated, it is approximately universal for quantum computation, meaning that we can get arbitrarily close to any $n$-qubit unitary using polynomially many Clifford+T gates (see the survey paper by Miller-Bakewell).

Since quantum circuits can be composed both 'horizontally' (do one process after another) and 'vertically' (do operations on multiple qubits at the same time), monoidal categories are a suitable algebraic framework for formalising this situation.

There have been two main approaches for developing an algebraic theory of quantum circuits. Relaxing the unitarity condition, we can consider arbitrary linear maps on qubits, which have been axiomatised in the ZX and ZW calculi, in terms of compact closed monoidal categories. These calculi are essentially graph-theoretic, which allows techniques from graph theory to be used for rewriting circuits (see e.g. the recent paper by Duncan et al.). The drawback of this approach is that it requires tools for unitary circuit extraction, because the instructions for a quantum computer are sequences of basic unitary operations.

A direct axiomatisation of unitary circuits, in the form of a symmetric monoidal groupoid, is a harder task because of the rigidity of such a representation. Moreover an axiomatisation of the full Clifford+T gate set with a finite number of relations is likely to be rather tricky, if possible at all, because of the inherent complexity of these circuits. For this reason, research has focused at axiomatising restricted fragments of the standard circuit model.

This was started in 2003 by Lafont, who provided a normal form for affine circuits generated by the $C N O T$ and $X$ gates. In 2015, Selinger gave a finite presentation for the Clifford groupoid, generated by $C N O T$, $X$, $H$ and $T^2$. Clifford gates are known to be efficiently simulatable classically, although adding any non-Clifford gate to the set allows to recover universal quantum computation. Non-Clifford gates, such as the $T$-gate, usually require a large number of resources to be implemented fault-tolerantly in a lab. For this reason a lot of current research has been looking for ways of reducing the $T$-count, i.e. the number of $T$-gates used in a circuit. To this end, Amy et al. (2013, 2016) introduced the formalism of phase polynomials for optimizing the $T$-count within the $\{C N O T, T\}$ -fragment.

Putting together the work of Lafont, the groupoid formalism of Selinger and the phase polynomials of Amy et al., the current paper provided a finite presentation of the CNOT-dihedral fragment, which is generated by $C N O T$, $X$ and $T$.

Brief overview of the paper

The paper proves existence and uniqueness of a normal for the CNOT-dihedral operators, which are defined below [Amy, Chen and Ross. p.86].

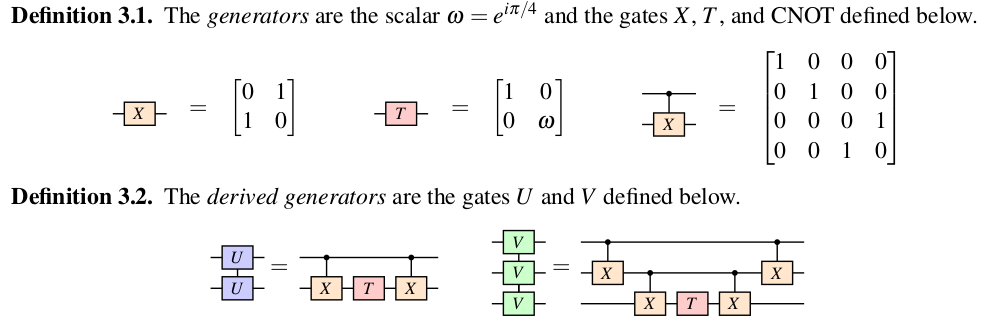
In addition to the above operators, we also have access to the $S W A P$ gate which corresponds to the linear map $|00\rangle \mapsto |00 \rangle$, $|01\rangle \mapsto |10 \rangle$, $|10\rangle \mapsto |01\rangle$, $|11\rangle \mapsto |11\rangle$ (where $|0\rangle$ and $|1\rangle$ denote the standard basis vectors), interchanging the position of two qubits. These gates generate a symmetric monoidaḷ groupoid where the monoidal product is given by the tensor product of matrices, the symmetry is given by the $S W A P$ gate and the invertibility of the generators can easily be checked.

An important step towards the normal form is the observation that the operators can be split into two classes: diagonal gates and affine gates. The diagonal gates have diagonal matrix representations, while the affine gates are affine transformations of the basis states. The gates $X$, $C N O T$ and $S W A P$ are affine, while $\omega$, $T$, $U$ and $V$ are diagonal. Those CNOT-dihedral circuits that only contain affine gates are called affine circuits, and correspondingly for diagonal circuits.

The CNOT-dihedral gates are subject to the following relations. [Amy, Chen and Ross. p.87].

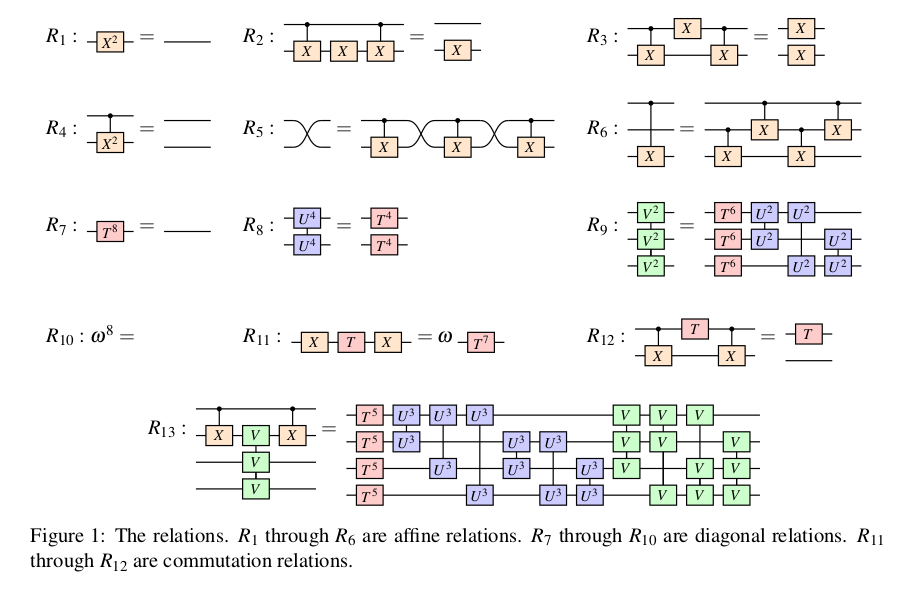
One central point to notice here are the degree reduction rules $R_1$, $R_4$, $R_7$, $R_8$, $R_9$ and $R_{10}$, which yield an upper bound on the power of each gate in the normal form (the power of a gate is just the number of times the gate is composed with itself). In fact $R_{13}$ can also be seen as a degree reduction rule; it shows that if we try to generalise the construction of $U$ and $V$ gates to four qubits, then this composite gate has degree zero (and hence there is no need to generalise beyond three qubits). The degree reduction rules also have a direct interpretation in terms of phase polynomial equalities, which we will discuss in more detail in a later section.

The overall normal form of a CNOT-dihedral circuit is a combination of the normal forms for an affine circuit and for a diagonal circuit. In fact, existence and uniqueness of the normal form for affine circuits was already proved by Lafont. Thus, what is proved in the present paper is that

• if an affine gate is to the left of a diagonal gate, the circuit can be rewritten in such a way that the affine gate is the rightmost gate and all the remaining gates are diagonal (i.e. affine gates ‘commute’ past the diagonal ones),

• diagonal gates commute with diagonal gates,

• any diagonal circuit has a unique normal form.

It then follows that any CNOT-dihedral circuit $C$ can be rearranged so that $C = D A$, where $D$ is a diagonal circuit and $A$ is an affine circuit. Then one can just apply the result of Lafont to $A$ and the last bullet point above to $D$ to get that $C$ has a unique normal form.

The diagonal normal form found in the paper is given by an ordering of the diagonal gates, together with bounds on the number of consecutive gates used, which come from their representation in terms of phase polynomials.

From ZX to CNOT-dihedral rules

In order to get an intuition for the presentation given in the paper, we make a short digression to introduce some of the ZX-calculus rules. This will allow us to understand the relations exposed in the paper as direct consequences of the underlying rules for linear maps modelled with the ZX-calculus. It will also highlight the rules which are not easily derivable from ZX, which we will see come from the phase polynomial formalism.

The ZX calculus is a diagrammatic language for complex linear maps based on (strongly) complementary bases, roughly meaning that measurements cannot be performed simultaneously in both bases. Generators in these bases are denoted by dots of different colour, traditionally red and green, decorated with a phase. The generators (known as spiders)

with $n$ inputs and $m$ outputs (the diagrams are read from left to right) correspond to linear maps

where $| \pm \rangle = \frac{1}{\sqrt 2}(|0\rangle \pm |1\rangle)$ and $\alpha\in(-\pi,\pi]$ (see e.g. Backens or Miller-Bakewell for a proper definition). The spiders can be thought of as generalised rotations; indeed, for a single qubit (n=m=1) the green spider corresponds to a rotation of the Bloch sphere of degree $\alpha$ around the Z axis, whereas the red spider is a rotation of degree $\alpha$ around the X axis.

The rule governing the interaction between generators of the same colour is the spider fusion law (a consequence of the axioms of dagger special Frobenius algebras), which states that spiders of the same colour can fuse into each other and their phases add up (modulo $2\pi$). This is in analogy with rotations: two consecutive rotations (around the same axis) correspond to one rotation by an angle which is just the sum of the two angles, and going a full turn gets you back to where you started. Be aware, however, that the analogy with rotations breaks down when we consider spiders with more than one input or output wire.

The basic rules encoding strong complementarity are the bialgebra and Hopf laws.

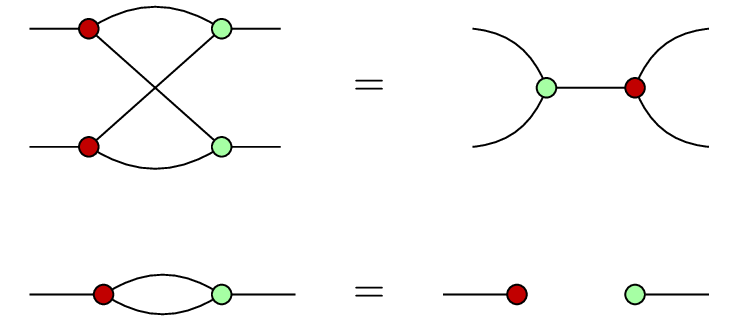
Note that we are using the scalarless version of the ZX calculus, i.e. the equalities between our ZX diagrams are only true up to a complex scalar. Even though the presentation given in the paper includes scalars (generated by $\omega$), these are not relevant for the operational intuition we want to convey with ZX diagrams.

The CNOT-dihedral fragment can be expressed in ZX, it is given by the following representations of the generators.

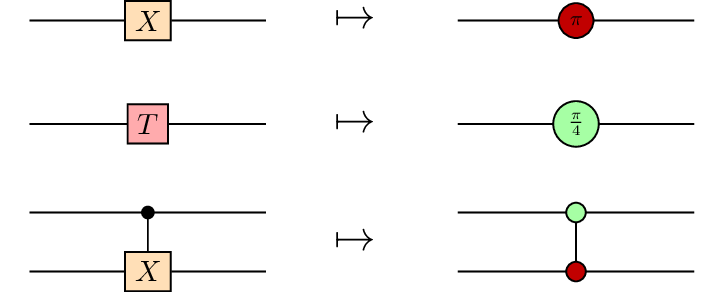
This can then be used to obtain the representations for the derived generators.

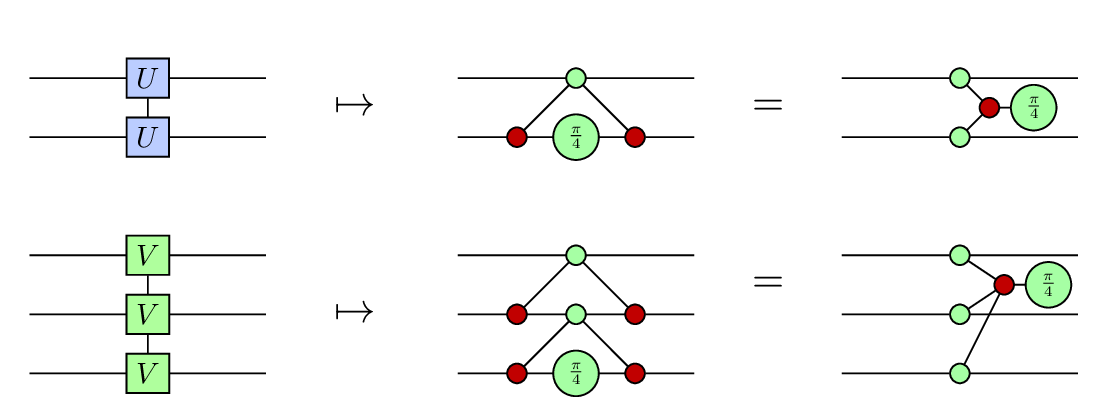
Given the interpretation of the ZX generators as rotations, the relations $R_1$ and $R_7$ now acquire a physical meaning; rotating by $\pi$ twice is the same as doing nothing, and likewise rotating by $\frac{\pi}{4}$ eight times is the same as doing nothing.

Most of the relations $R_1$ to $R_{13}$ can be derived using the spider fusion law, the Hopf law and the bialgebra law. Rules 9 and 13 are the least straightforward, in fact we don’t know of any direct derivation of rule 13 from the axioms, although by the recent completeness results for the ZX calculus such a derivation must exist (there has recently been a wealth of completeness results for ZX; see the survey by Miller-Bakewell). Those rules however have a direct interpretation in terms of their phase polynomial representation.

Diagonal gates and phase polynomials

The action of any diagonal gate from the CNOT-dihedral fragment can be described as follows: $$D |x\rangle = \omega^{p_D(x)}|x\rangle, \quad p_D: \mathbb{Z}_2^n \rightarrow \mathbb{Z}_8 ,$$ Where $p_D$ is a polynomial using mixed arithmetic: $$p_D(x) = \sum_{i=1}^k a_i g_i(x)$$ where $a_i \in \mathbb{Z}_8$ and $g_i:\mathbb{Z}_2^n \rightarrow \mathbb{Z}_2$ are linear terms on at most $n$ variables, i.e terms of the form $x_{i_1} \oplus \dots \oplus x_{i_k}$ for some $k \leq n$ (this was shown in Amy et al.). Representations for the generating diagonal gates are given by:

$$\omega^k |x\rangle = \omega^k |x\rangle$$ $$T^k |x_1\rangle = \omega^{kx_1}|x_1\rangle$$ $$U^k |x_1x_2\rangle = \omega^{k(x_1\oplus x_2)}|x_1x_2\rangle$$ $$V^k |x_1x_2x_3\rangle = \omega^{k(x_1\oplus x_2 \oplus x_3)}|x_1x_2x_3\rangle$$

We can read off the phase polynomial of a circuit on $n$ qubits built from the diagonal generators by labelling each wire with an index $i=1,2, \dots, n$ (from top to bottom say) and adding: a constant term $1$ for each scalar $\omega$, a term $x_i$ whenever $T$ is applied to qubit $i$, a term $x_i \oplus x_j$ whenever $U$ is applied to qubits $i$ and $j$ and a term $x_i \oplus x_j \oplus x_k$ whenever $V$ is applied to qubits $i$,$j$ and $k$. Note that the order doesn’t matter as diagonal gates commute. So we obtain the following general form:

$$p_D(x) = a_0 + \sum_i a_i x_i + \sum_{i \lt j} b_{i j} (x_i \oplus x_j) + \sum_{i \lt j \lt k}c_{i j k} (x_i \oplus x_j \oplus x_k)$$

The important thing to note is that from the degree-reduction rules discussed earlier, the coefficients in the expression above can be bounded: $a_i \in \mathbb{Z}_8$, $b_{i j} \in \mathbb{Z}_4$, $c_{i j k} \in \mathbb{Z}_2$. For instance if four $U$ gates are applied on the same pair of qubits, we can use rule 8 to turn them into $T$ gates.

This leads directly to a definition of the diagonal normal form, given by ordering the gates as they appear on the phase polynomial representation. The existence of the normal form comes from the fact that diagonal gates commute and that they are generated by $\omega$, $T$, $U$ and $V$. The bounds on coefficients $a_i, b_{i j}$ and $c_{i j k}$ are the main ingredient to prove uniqueness.

The proof of uniqueness for the diagonal normal form proceeds as follows. Suppose $D$ and $D'$ are distinct diagonal normal forms, we want to show that they differ on some input, that is, there is a $y \in \mathbb{Z}_2^n$ such that $D|y\rangle \neq D'|y\rangle$. By construction, $p_D(x) \neq p_{D'}(x)$ as polynomials. However, because of the use of mixed arithmetic in the polynomial expression, this does not mean that there is a $y \in \mathbb{Z}_2^n$ such that $p_D(y) \neq p_{D'}(y)$. The following is a counterexample: $4x_1 + 4x_2 + 4(x_1 \oplus x_2) = 0$ mod $8$ for any $x_1, x_2 \in \mathbb{Z}_2$. However, because of the bounds on the coefficient $a_i$, $b_{i j}$ and $c_{i j k}$, it can be shown that this situation never occurs, and that in fact there is a $y \in \mathbb{Z}_2^n$ such that $D|y\rangle \neq D' |y\rangle$.

Towards $T$-count optimization in ZX circuits.

We have seen that phase polynomials are a useful technique for normalising diagonal circuits and distinguishing between them. Degree reduction rules and rule 13 in the paper are directly imported from this formalism. We have seen that most of those rules can be derived straightforwardly from the ZX calculus, except for $R_{13}$, for which no direct derivation is known. The content of this section is inspired by a discussion with Quanlong Wang, we analyse $R_{13}$ from a ZX perspective, and show how it can be used to reduce T-count in ZX circuits.

First note that $R_{13}$ has the following phase polynomial representation: $$x_1 \oplus x_2 \oplus x_3 \oplus x_4 = \sum_i 5x_i + \sum_{i\lt j} 3(x_i \oplus x_j) + \sum_{i\lt j\lt k}x_i \oplus x_j \oplus x_k.$$ Reasoning inductively from this equality we can see that whenever a phase polynomial has terms with more than four variables, it can be rewritten as a phase polynomial where each term has at most three variables. This explains why $\omega$, $T$, $U$ and $V$ generate all diagonal gates. In normalising CNOT-dihedral gates, this rule is used ‘from left to right’, in order to commute the CNOT gate to the left of the diagonal gates.

Now note that $R_{13}$ corresponds to the following equality of ZX circuits:

From the representation above, we see that the right-hand side contains $14= \sum_{i=1}^3{\binom{4}{i}}$ occurrences of (an odd multiple of) $\frac{\pi}{4}$ rotations, whereas the left-hand side contains only one. As discussed in the introduction, $\frac{\pi}{4}$ rotations (i.e. $T$-gates) are hard to implement in a fault-tolerant way. In order to reduce the $T$-count we want to use $R_{13}$ ‘from right to left’. To do this let us consider the fragment of diagonal $ZX$ circuits, i.e. $ZX$ diagrams with $n$ inputs and $n$ outputs generated by $\omega$, $T$, $U$ and $V$. Define the $T$-count of a diagonal ZX circuit to be the number of (odd multiples of) $\frac{\pi}{4}$ phases appearing in the diagram. Let us also call ‘phase gadget’ a diagram of the form:

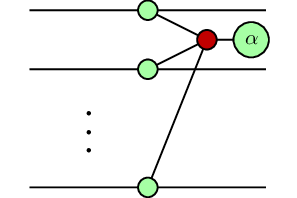
As diagonal gates commute amongst themselves, we can think of any diagonal ZX circuit $D:n \rightarrow n$ as a hypergraph with $n$ nodes and labelled hyperedges for each phase gadget. Then $R_{13}$ can be generalised roughly as follows: any diagonal ZX circuit on $4$ qubits (seen as a hypergraph) is equivalent to the hypergraph where the connections have been complemented and an additional phase gadget is connected to all 4 nodes. The labels on the phase gadgets should also be modified appropriately, but we don’t go into detail here.

This yields the following rewrite procedure for reducing $T$-count in diagonal ZX circuits. Given an arbitrary diagonal ZX circuit $D: n \rightarrow n$, choose any quadruple of input qubits and consider the sub-hypergraph of hyperedges connected only to those 4 nodes. If the $T$-count of the sub-hypergraph is $k\gt 7$, then we can use the generalised $R_{13}$ to complement all the connections and add a phase gadget connected to all 4 nodes. Then the $T$-count of the sub-hypergraph has been reduced from $k$ to $14-k+1$, reducing the overall $T$-count of $D$ by $k-8$.

Future directions

As the authors of the paper remark in the conclusion, their result does not provide an algorithm to rewrite an arbitrary CNOT-dihedral circuit, as the coherence axioms of a symmetric monoidal category are non-constructive. Thus the next natural question to ask is how to find such an algorithm.

By removing the $X$ gate from the gate set considered in the paper, one obtains a normal form for the gate set $\{C N O T, T\}$. Thus the only gate missing in order to turn this into the Clifford+T gate set is the Hadamard gate. Since the Clifford+T gate set is known to be approximately universal for quantum computation, it would be of great interest to know whether there is a normal form for this fragment as well. This is currently an open problem. However, the authors make a combinatorial argument showing that including the Hadamard gate increases the number of diagonal gates dramatically. This suggests that the solution, even if it exists, is not an easy generalisation of the results of the paper.

In the last section, we saw how the phase polynomial identity for $R_{13}$ can be used to simplify ZX-circuits. Amy et al. (2016) classified all phase polynomial equalities (analogous to $R_{13}$) in terms of Reed-Muller codes, translating those identities to develop rewrite techniques for $T$-count optimization in ZX circuits is a promising direction of future research.