Musings

Chiefly, the polarization data lets you pin down the (integrated) optical depth, $\tau$, where $$\tau(z) = c \sigma_T \int_0^z n_e(z') (dt/dz') dz'$$ $\sigma_T$ is the cross section for Thompson scattering, $n_e(z)$ is the number density of free electrons.

Before decoupling (at $z\sim 1088$), the optical depth, $d\tau/d z \gg 1$. After decoupling, it drops to near zero. Then, at reionization (when the first stars turn on), it goes back up. Polarization of the CMB is created at decoupling, due to velocity gradients in the primordial plasma. At reionization (somewhere between $11\lesssim z_r \lesssim 30$), again, polarization is created as the free electrons scatter off the quadrupole moment of the incident CMB photons. The latter effect produced polarization primarily in low-$l$, and is cleanly distinguishable from the “primordial” polarization created at decoupling.

With WMAP-3, they were able to determine $\tau(z_r)$ at reionization. With a few more years of data, Eiichiro says they will actually be able to measure $\tau(z)$.

By measuring $\tau$, one breaks a degeneracy in the determination of the cosmological parameters from the temperature alone. For instance, just looking at the temperature data, a larger $\tau$ can be compensated by (among other things) larger values of the tilt, $n_s$, and of the tensor-scalar ratio, $r$. Once you pin down $\tau$, you narrow the window for these cosmological parameters.

Eiichiro ended his talk with this graph:

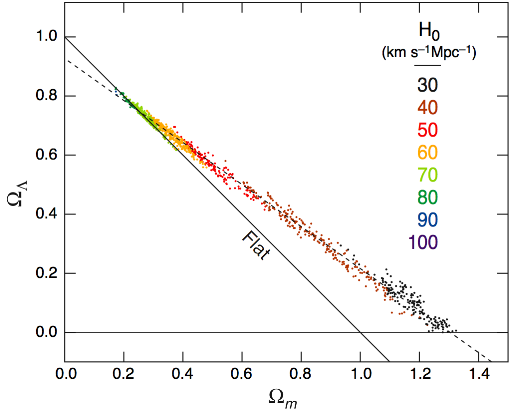
Range of non-flat cosmology models consistent with the WMAP data only. The models in the figure are all power-law CDM models with dark energy and dark matter, but without the constraint that $\Omega_\Lambda+\Omega_m=1$. The different colors correspond to values of the Hubble constant as indicated in the figure. (WMAP Three Year Results: Implications for Cosmology)

mostly to show that, from WMAP data alone, one learns that $\Lambda=0$ requires a ridiculously low value of the Hubble constant. But what really leaps out at you is that the WMAP data seems to favour positive spatial curvature (a “closed” FRW universe).

This tendency is somewhat diminished when you combine WMAP with other datasets:

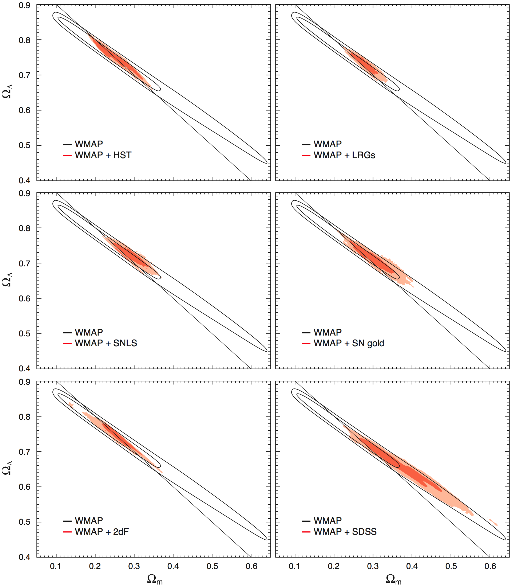
Joint two-dimensional marginalized contours (68% and 95%) for matter density, $\Omega_m$, and vacuum energy density, for power-law CDM models with dark energy and dark matter, but without the constraint that $\Omega_\Lambda+\Omega_m=1$. The panels show various combinations of WMAP and other data sets. While models with $\Omega_m = 0.415$ and $\Omega_\Lambda= 0.630$ are a better fit to the WMAP three year data alone than the flat model, the combination of WMAP three year data and other astronomical data favors nearly flat cosmologies. (WMAP Three Year Results: Implications for Cosmology)

The combined data favour a universe that is nearly spatially flat. But it does seem that the bulk of the allowed parameter space lies in the region of positive spatial curvature¹.